An example Chi-Tech cross section file is shown below. The bare-bones format is shown below with more examples below:
# This header can be as large as you please. The actual processing
# starts at NUM_GROUPS as the first word. After that, NUM_MOMENTS needs to
# be processed before any of the other keywords.
NUM_GROUPS 2
NUM_MOMENTS 2
SIGMA_T_BEGIN
0 0.5
1 0.5
SIGMA_T_END
Comments
TRANSFER_MOMENTS_BEGIN
#Zeroth moment (l=0)
M_GPRIME_G_VAL 0 0 0 0.01
M_GPRIME_G_VAL 0 0 1 0.09
M_GPRIME_G_VAL 0 1 1 0.08
#(l=1)
M_GPRIME_G_VAL 1 0 0 -0.001
M_GPRIME_G_VAL 1 0 1 0.001
M_GPRIME_G_VAL 1 1 1 0.001
TRANSFER_MOMENTS_END
Steady state simulations:
The cross sections can be used in simulations solving the steady state Linear Boltzmann Equation of the form:
![\[ \vec{\Omega}_n \boldsymbol{\cdot} \vec{\nabla} \psi_{ng} + \sigma_{tg} \psi_{ng} = \sum_{\ell=0}^L \sum_{m=-\ell}^{+\ell} \frac{2\ell+1}{4\pi} Y_{\ell m} (\vec{\Omega}_n) \sum_{g'=0}^{G-1} \sigma_{s\ell,g'{\to}g} \phi_{\ell m,g'} + q_{ext,ng} + q_{fission,ng} \]](../../form_94.png)
The two most prominent items required here includes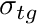 
and 
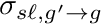. The latter is an entry in a structure we call a generic transfer matrix for moment 
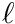with rows 
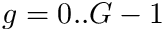and columns 
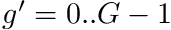. These two items are often the only items required in a transport simulation.
In simulations with fission-sources, cross sections support two formats, the simple combined cross sections without delayed neutrons
![\[ q_{fission,ng} = \frac{\chi_g}{4\pi} \sum_{g'=0}^{G-1} \nu_{g'} \sigma_{fg'} \phi_{00g'} \]](../../form_99.png)
and those with delayed neutrons, the latter which are currently only used in the k-eigenvalue solver.
k-eigenvalue related items
As stated before, the cross section file supports two formats, the simple combined cross sections without delayed neutrons which are depicted above and those with delayed neutrons shown below
![\[ q_{fission,ng} = \frac{\chi_g}{4\pi} \sum_{g'=0}^{G-1} \nu_{prompt,g'} \sigma_{fg'} \phi_{00g'} + \sum_{j=0}^{J-1} \frac{\chi_{delayed,jg}}{4\pi} \gamma_j \sum_{g'=0}^{G-1} \nu_{delayed,g'} \sigma_{fg'} \phi_{00g'} \]](../../form_100.png)
.
Codes may also choose to update precursor concentrations for which their decay constants,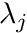 
are required.
Keyword definitions
- NUM_GROUPS num_groups Required. Specifies the number of groups for this cross section. Symbol
.
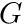- NUM_MOMENTS num_moments Required. The number of transfer matrices to allocate for this cross section (whether used or not). Typically this number is one greater than the scattering order (i.e.,
)
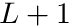- NUM_PRECURSORS num_precursors Optional. Indicates how many precursors are used in this cross section. Symbol
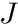
- Optional key words per line:
- SIGMA_T_BEGIN. Optional. Starts a block that is terminated by a line SIGMA_T_END. Each line in the block processes the first two words as [group, sigma_t]. Populates the sigma_tg field. Symbol .
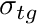- SIGMA_A_BEGIN. Optional. Starts a block that is terminated by a line SIGMA_A_END. Each line in the block processes the first two words as [group, sigma_a]. Populates the sigma_ag field. Symbol
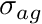. If this is not supplied then sigma_a is estimated from the transfer matrix and may erroneously estimate balance.
- SIGMA_F_BEGIN. Optional. Starts a block that is terminated by a line SIGMA_F_END. Each line in the block processes the first two words as [group, sigma_f]. Populates the sigma_fg field. Symbol
.
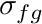- NU_BEGIN. Optional. Starts a block that is terminated by a line NU_END. Each line in the block processes the first two words as [group, nu]. Populates the nu field. Upon completing the file processing the nu_sigma_fg field gets populated from the product of nu and sigma_fg. Symbol
.
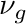- NU_PROMPT_BEGIN. Optional. Starts a block that is terminated by a line NU_PROMPT_END. Each line in the block processes the first two words as [group, nu_prompt]. Populates the nu_prompt field. Upon completing the file processing the nu_p_sigma_fg field gets populated from the product of nu_prompt and sigma_fg. Symbol
.
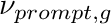- NU_DELAYED_BEGIN. Optional. Starts a block that is terminated by a line NU_DELAYED_END. Each line in the block processes the first two words as [group, nu_delayed]. Populates the nu_delayed field. Upon completing the file processing the nu_d_sigma_fg field gets populated from the product of nu_delayed and sigma_fg. Symbol
.
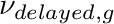- CHI_BEGIN. Optional. Starts a block that is terminated by a line CHI_END. Each line in the block processes the first two words as [group, chi]. Populates the chi field. Symbol
.
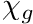- CHI_PROMPT_BEGIN. Optional. Starts a block that is terminated by a line CHI_PROMPT_END. Each line in the block processes the first two words as [group, chi]. Populates the chi_prompt field. Symbol
.
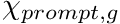- VELOCITY_BEGIN. Optional. Starts a block that is terminated by a line VELOCITY_END. Each line in the block processes the first two words as [group, velocity]. Populates the inv_velocity field by inverting parsed values. Symbol
.
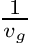- INV_VELOCITY_BEGIN. Optional. Starts a block that is terminated by a line INV_VELOCITY_END. Each line in the block processes the first two words as [group, inv_velocity]. Populates the inv_velocity field. If this field and VELOCITY are provided, this field will be used. Symbol .
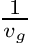- PRECURSOR_DECAY_CONSTANTS_BEGIN. Optional. Starts a block that is terminated by a line PRECURSOR_DECAY_CONSTANTS_END. Each line in the block processes the first two words as [precursor, lambda]. Populates the lambda field (the precursor decay constant). Symbol .
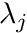- PRECURSOR_FRACTIONAL_YIELDS_BEGIN. Optional. Starts a block that is terminated by a line PRECURSOR_FRACTIONAL_YIELDS_END. Each line in the block processes the first two words as [precursor, gamma]. Populates the gamma field (the precursor production fraction per fission). Symbol
.
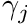- CHI_DELAYED_BEGIN. Optional. Starts a block that is terminated by a line CHI_DELAYED_END. Each line in the block processes the first word as the group index and the remaining NUM_PRECURSORS words as the the individual precursor's associated delayed spectrum (chi). Populates the chi_d field. Symbol
.
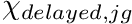- TRANSFER_MOMENTS_BEGIN. Optional. Starts a block that is terminated by a line TRANSFER_MOMENTS_END. Each line in the block processes a line only if it starts with the keyword M_GPRIME_G_VAL which needs to be followed by four values [moment,gprime,g,value]. Populates transfer-matrix for moment m, row g, column gprime, with value. Symbol .
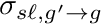- Comments can be between individual blocks but only the TRANSFER_MOMENTS block may have comments between the _BEGIN and _END
- Comments do not have to start with any specific character since the file format is keyword driven.
- Any number that is not convertible to its required type (integer, double) will throw an error to that effect.
- All errors will indicate the current file, line number and nature of the error.
More Advanced Examples
# This header can be as large as you please. The actual processing
# starts at NUM_GROUPS as the first word. After that, NUM_MOMENTS needs to
# be processed before any of the other keywords.
NUM_GROUPS 2
NUM_MOMENTS 2
NUM_PRECURSORS 3
SIGMA_T_BEGIN
0 0.5
1 0.5
SIGMA_T_END
Comments
SIGMA_F_BEGIN
0 0.01
1 0.40737
SIGMA_F_END
NU_PROMPT_BEGIN
0 2.45
1 2.45
NU_PROMPT_END
CHI_PROMPT_BEGIN
0 1.0
1 0.0
CHI_PROMPT_END
VELOCITY_BEGIN
0 2.2e10
1 272.145
VELOCITY_END
TRANSFER_MOMENTS_BEGIN
#Zeroth moment (l=0)
M_GPRIME_G_VAL 0 0 0 0.01
M_GPRIME_G_VAL 0 0 1 0.09
M_GPRIME_G_VAL 0 1 1 0.08
#(l=1)
M_GPRIME_G_VAL 1 0 0 -0.001
M_GPRIME_G_VAL 1 0 1 0.001
M_GPRIME_G_VAL 1 1 1 0.001
TRANSFER_MOMENTS_END
PRECURSOR_DECAY_CONSTANTS_BEGIN
0 0.1
1 0.2
2 0.3
PRECURSOR_DECAY_CONSTANTS_END
PRECURSOR_GAMMA_BEGIN
0 0.25
1 0.5
2 0.25
PRECURSOR_GAMMA_END
NU_DELAYED_BEGIN
0 0.01
1 0.02
2 0.01
NU_DELAYED_END
CHI_DELAYED_BEGIN
G_PRECURSOR_VAL 0 0 1.0
G_PRECURSOR_VAL 0 1 1.0
G_PRECURSOR_VAL 0 2 1.0
G_PRECURSOR_VAL 1 0 0.0
G_PRECURSOR_VAL 1 1 0.0
G_PRECURSOR_VAL 1 2 0.0
CHI_DELAYED_END
1.9.3