Table of contents
1 Poisson's equation
The Poisson's equation states the following, for 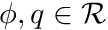 ,
,
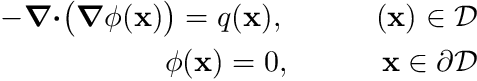
where  denotes the divergence-operator and
denotes the divergence-operator and  denotes the gradient-operator, i.e.
denotes the gradient-operator, i.e.  denotes the gradient of
denotes the gradient of 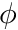 . The boundary conditions here state that
. The boundary conditions here state that 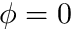 on the boundary.
on the boundary.
1.1 Our specific problem
For our specific problem we will choose 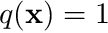 and
and 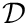 a cartesian domain, either 1D, 2D or 3D, with each dimension always between
a cartesian domain, either 1D, 2D or 3D, with each dimension always between 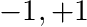 . We can generate the mesh for this problem using an input file
. We can generate the mesh for this problem using an input file
--############################################### Setup mesh
mesh={}
N=20
L=2
xmin = -L/2
dx = L/N
for i=1,(N+1) do
k=i-1
mesh[i] = xmin + k*dx
end
--###############################################
Set Material IDs
Handle chiMeshHandlerCreate()
Two chiMeshCreateUnpartitioned3DOrthoMesh(array_float x_nodes, array_float y_nodes, array_float z_nodes)
Two chiMeshCreateUnpartitioned2DOrthoMesh(array_float x_nodes, array_float y_nodes)
Two chiMeshCreateUnpartitioned1DOrthoMesh(array_float x_nodes)
void chiVolumeMesherSetMatIDToAll(int material_id)
void chiVolumeMesherExecute()
void Set(VecDbl &x, const double &val)
This code can be used to generate any of the following meshes,
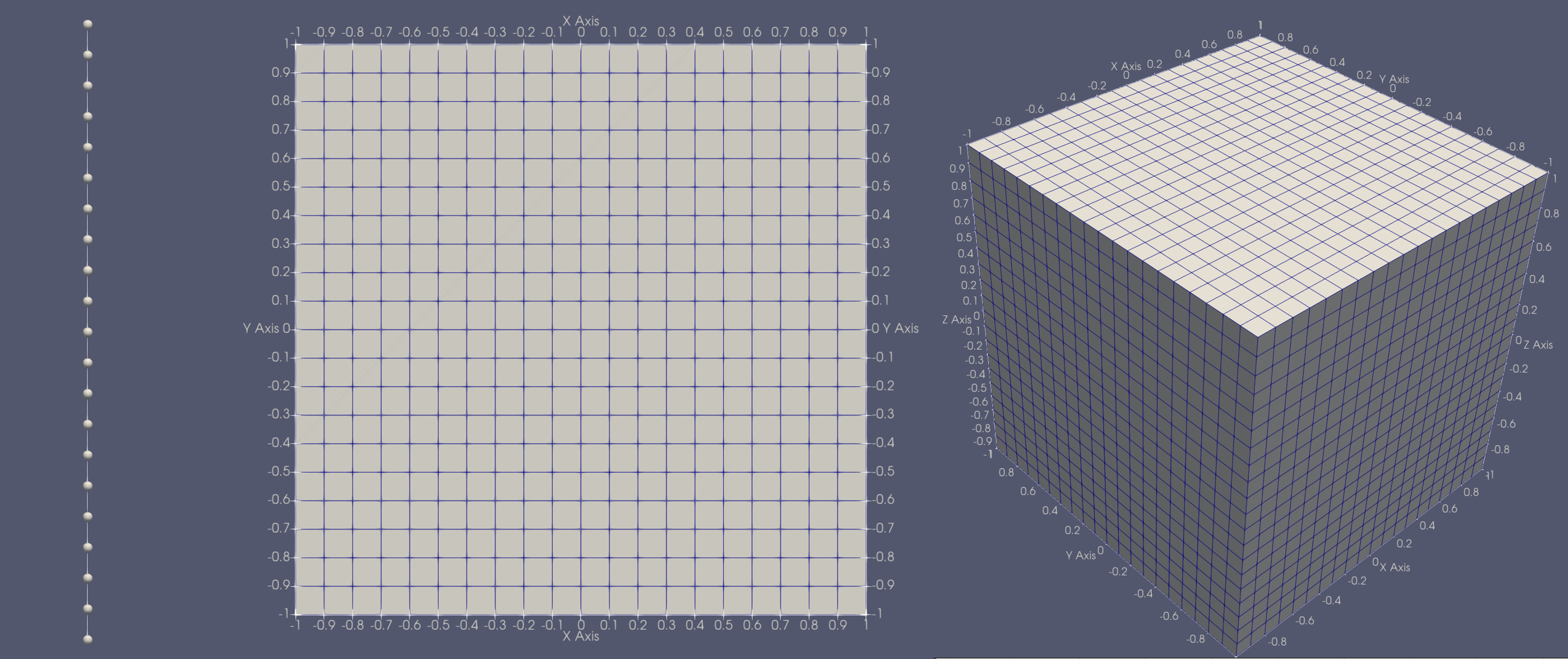
[From left to right] 1D, 2D, 3D orthogonal mesh
1.2 The Weak-form of Poisson's equation
When using the finite element method we develop the so-called weak-form by weighting the Poisson equation with a trial space function, 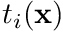 , where
, where 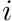 is a unique node in the problem, and then integrate over the volume of the domain
is a unique node in the problem, and then integrate over the volume of the domain
![\[ -\int_V t_i \boldsymbol{\nabla} \boldsymbol{\cdot} \bigr(\boldsymbol{\nabla} \phi(\mathbf{x})\bigr) dV = \int_V t_i q(\mathbf{x}) dV. \]](../../form_157.png)
Next we apply integration by parts to the left term, for which,
![\[ t_i \boldsymbol{\nabla} \boldsymbol{\cdot} \bigr(\boldsymbol{\nabla} \phi(\mathbf{x})\bigr) = \boldsymbol{\nabla} \cdot (t_i \boldsymbol{\nabla} \phi) - (\boldsymbol{\nabla} t_i ) \boldsymbol{\cdot} (\boldsymbol{\nabla} \phi) \]](../../form_158.png)
which gives
![\[ \int_V (\boldsymbol{\nabla} t_i ) \boldsymbol{\cdot} (\boldsymbol{\nabla} \phi) dV -\int_V \boldsymbol{\nabla} \boldsymbol{\cdot} (t_i \boldsymbol{\nabla} \phi) dV = \int_V t_i q(\mathbf{x}) dV. \]](../../form_159.png)
We then apply Gauss's Divergence Theorem to the second term from the left, to get
![\[ \int_V (\boldsymbol{\nabla} t_i ) \boldsymbol{\cdot} (\boldsymbol{\nabla} \phi) dV -\int_S \mathbf{n} \boldsymbol{\cdot} (t_i \boldsymbol{\nabla} \phi) dA = \int_V t_i q(\mathbf{x}) dV. \]](../../form_160.png)
This is essentially the weak-form.
1.3 The discretized equation with the Continuous Galerkin approach
To fully discretize this equation we next approximate the continuous nature of 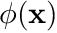 using essentially a very fancy interpolation scheme. With this scheme we approximate
using essentially a very fancy interpolation scheme. With this scheme we approximate 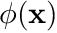 as
as 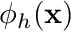 where
where
![\[ \phi(\mathbf{x}) \approx \phi_h(\mathbf{x}) = \sum_j \phi_j b_j(\mathbf{x}) \]](../../form_163.png)
where the coefficients 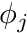 do not dependent on space and
do not dependent on space and 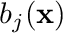 are called shape functions. For this tutorial we will be utilizing the Piecewise Linear Continuous (PWLC) shape functions which are generally specially in the fact that they can support arbitrary polygons and polyhedra.
are called shape functions. For this tutorial we will be utilizing the Piecewise Linear Continuous (PWLC) shape functions which are generally specially in the fact that they can support arbitrary polygons and polyhedra.
We will also follow a Galerkin approach, resulting in the trial-functions 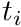 being the same as the shape functions, i.e.,
being the same as the shape functions, i.e., 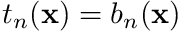 .
.
With this approximation defined, our weak form, after neglecting the surface integral since we have Dirichlet boundary conditions, becomes
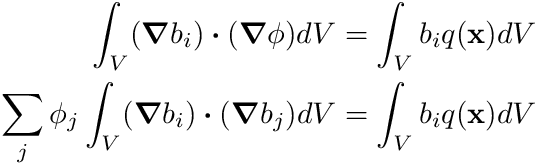
Now we are faced with the dilemma of how to compute the integral terms in this equation. The first thing we do here is to observe that the shape functions 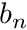 are defined cell-by-cell, therefore we can drill a little deeper by defining
are defined cell-by-cell, therefore we can drill a little deeper by defining
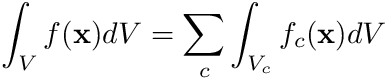
where 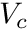 is the volume of cell
is the volume of cell 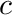 . The function
. The function 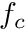 is a function uniquely defined within cell
is a function uniquely defined within cell 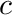 's volume.
's volume.
These integrals are often difficult to perform in real-world coordinates and are therefore carried out on a reference element in a different coordinate system. This necessitates the use of a transformation using the magnitude of the Jacobian that transforms the above integrals into the form
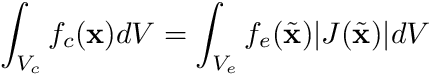
where 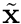 is position in the reference coordinate frame,
is position in the reference coordinate frame, 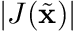 is the magnitude of the Jacobian,
is the magnitude of the Jacobian, 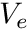 is the volume of the reference element, and
is the volume of the reference element, and 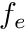 is the reference element equivalent of
is the reference element equivalent of 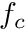 . Now, the big advantage of doing this is that we can use quadrature rules for these integrals
. Now, the big advantage of doing this is that we can use quadrature rules for these integrals
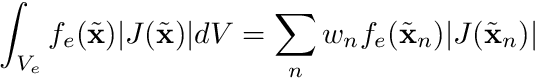
where 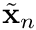 are the abscissas of the quadrature rule and
are the abscissas of the quadrature rule and 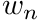 are the quadrature weights.
are the quadrature weights.
With these mathematical formulations defined we can write
![\begin{align*} \sum_j \phi_j \sum_c \sum_n^{N_V} \biggr[ w_n (\boldsymbol{\nabla} b_i(\tilde{\mathbf{x}}_n) ) \boldsymbol{\cdot} (\boldsymbol{\nabla} b_j(\tilde{\mathbf{x}}_n)) |J(\tilde{\mathbf{x}}_n)| \biggr] &= \sum_c \sum_n^{N_V} w_n b_i(\tilde{\mathbf{x}}_n) q(\tilde{\mathbf{x}}_n \to \mathbf{x}) |J(\tilde{\mathbf{x}}_n)| \end{align*}](../../form_182.png)
2 Setting up the problem
For this tutorial we basically follow the flow of Coding Tutorial 1 - Poisson's problem with Finite Volume. Make sure you make sensible changes to the CMakeLists.txt file and name your source file appropriately, which for me is code_tut3.cc.
The first portion of the tutorial is the same. We create a mesh.lua file in the chi_build directory. We get the grid
int main(
int argc,
char* argv[])
{
chi::Initialize(argc,argv);
chi::RunBatch(argc, argv);
chi::log.Log() << "Coding Tutorial 3";
const auto& grid = *grid_ptr;
chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
int main(int argc, char **argv)
chi_mesh::MeshContinuumPtr & GetGrid() const
MeshHandler & GetCurrentHandler()
3 Initializing the PWLC Spatial Discretization
To gain access to the chi_math::SpatialDiscretization_PWLC class we need to include the header
#include "math/SpatialDiscretization/FiniteElement/PiecewiseLinear/pwlc.h"
Next we add the following code
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_PWLC::New(grid_ptr);
const auto& sdm = *sdm_ptr;
const auto& OneDofPerNode = sdm.UNITARY_UNKNOWN_MANAGER;
const size_t num_local_dofs = sdm.GetNumLocalDOFs(OneDofPerNode);
const size_t num_globl_dofs = sdm.GetNumGlobalDOFs(OneDofPerNode);
chi::log.Log() << "Num local DOFs: " << num_local_dofs;
chi::log.Log() << "Num globl DOFs: " << num_globl_dofs;
std::shared_ptr< SpatialDiscretization > SDMPtr
The initialization of the matrices and vectors remain exactly the same as in the Finite Volume tutorial:
const auto n = static_cast<int64_t>(num_local_dofs);
const auto N = static_cast<int64_t>(num_globl_dofs);
std::vector<int64_t> nodal_nnz_in_diag;
std::vector<int64_t> nodal_nnz_off_diag;
sdm.BuildSparsityPattern(nodal_nnz_in_diag,nodal_nnz_off_diag, OneDofPerNode);
nodal_nnz_in_diag,
nodal_nnz_off_diag);
void InitMatrixSparsity(Mat &A, const std::vector< int64_t > &nodal_nnz_in_diag, const std::vector< int64_t > &nodal_nnz_off_diag)
Mat CreateSquareMatrix(int64_t local_size, int64_t global_size)
Vec CreateVector(int64_t local_size, int64_t global_size)
4 Using quadrature data to assemble the system
With the finite element method the conventional way to assemble the matrix is to do so by element (even though continuous FEM is only concerned about nodes). Therefore we start with a loop over elements then assemble our discretized equation
![\begin{align*} \sum_j \phi_j \sum_c \sum_n^{N_V} \biggr[ w_n (\boldsymbol{\nabla} b_i(\tilde{\mathbf{x}}_n) ) \boldsymbol{\cdot} (\boldsymbol{\nabla} b_j(\tilde{\mathbf{x}}_n)) |J(\tilde{\mathbf{x}}_n)| \biggr] &= \sum_c \sum_n^{N_V} w_n b_i(\tilde{\mathbf{x}}_n) q(\tilde{\mathbf{x}}_n \to \mathbf{x}) |J(\tilde{\mathbf{x}}_n)| \end{align*}](../../form_182.png)
For which the first portion of the code is
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto qp_data = cell_mapping.MakeVolumeQuadraturePointData();
const size_t num_nodes = cell_mapping.NumNodes();
VecDbl cell_rhs(num_nodes, 0.0);
for (size_t i=0; i<num_nodes; ++i)
{
for (size_t j=0; j<num_nodes; ++j)
{
double entry_aij = 0.0;
for (size_t qp : qp_data.QuadraturePointIndices())
{
entry_aij +=
qp_data.ShapeGrad(i, qp).Dot(qp_data.ShapeGrad(j, qp)) *
qp_data.JxW(qp);
}
Acell[i][j] = entry_aij;
}
for (size_t qp : qp_data.QuadraturePointIndices())
cell_rhs[i] += 1.0 * qp_data.ShapeValue(i, qp) * qp_data.JxW(qp);
}
std::vector< VecDbl > MatDbl
std::vector< double > VecDbl
The first thing we do here, as with any SD, is to grab the relevant cell mapping. After that we immediately create a chi_math::finite_element::InternalQuadraturePointData with the line of code
const auto qp_data = cell_mapping.MakeVolumeQuadraturePointData();
This data structure contains the shape function values, together with other data, pre-stored per quadrature point.
Next we create a local cell-matrix and local right-hand-side (RHS) which serve as lightweight proxies before we assemble relevant values into the global matrix and global RHS.
const size_t num_nodes = cell_mapping.NumNodes();
VecDbl cell_rhs(num_nodes, 0.0);
We then loop over all the 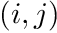 node combinations of our equation above but with scope only on the local element. Notice that we never actually pass around the actual quadrature points but rather use the quadrature point indices via
node combinations of our equation above but with scope only on the local element. Notice that we never actually pass around the actual quadrature points but rather use the quadrature point indices via qp_data.QuadraturePointIndices().
for (size_t i=0; i<num_nodes; ++i)
{
for (size_t j=0; j<num_nodes; ++j)
{
double entry_aij = 0.0;
for (size_t qp : qp_data.QuadraturePointIndices())
{
entry_aij +=
qp_data.ShapeGrad(i, qp).Dot(qp_data.ShapeGrad(j, qp)) *
qp_data.JxW(qp);
}
Acell[i][j] = entry_aij;
}
for (size_t qp : qp_data.QuadraturePointIndices())
cell_rhs[i] += 1.0 * qp_data.ShapeValue(i, qp) * qp_data.JxW(qp);
}
Notice that we are actually doing
![\begin{align*} \sum_j \sum_n^{N_V} \biggr[ (\boldsymbol{\nabla} b_i(\tilde{\mathbf{x}}_n) ) \boldsymbol{\cdot} (\boldsymbol{\nabla} b_j(\tilde{\mathbf{x}}_n)) w_n |J(\tilde{\mathbf{x}}_n)| \biggr] \end{align*}](../../form_184.png)
for cell 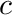 , where
, where 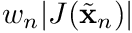 is combined into
is combined into qp_data.JxW(qp).
5 Compensating for Dirichlet boundaries
Dirichlet requires some special considerations. The equation for node 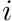 essentially becomes
essentially becomes 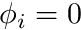 for our case of zero Dirichlet boundary conditions. This essentially places just a 1 on the diagonal with no entries off-diagonal for the entire row
for our case of zero Dirichlet boundary conditions. This essentially places just a 1 on the diagonal with no entries off-diagonal for the entire row 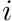 . Therefore, we need to modify the local cell-matrix to reflect this situation.
. Therefore, we need to modify the local cell-matrix to reflect this situation.
We are unfortunately not done yet. Any row in the matrix that has an off-diaganol entry that corresponds to column 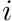 will need to be moved to the RHS. This is because it could destroy the symmetry of an otherwise symmetric matrix.
will need to be moved to the RHS. This is because it could destroy the symmetry of an otherwise symmetric matrix.
We handle both these modifications in the following way. We build a flag-list for each cell node
std::vector<bool> node_boundary_flag(num_nodes, false);
const size_t num_faces = cell.faces.size();
for (size_t f=0; f<num_faces; ++f)
{
const auto& face = cell.faces[f];
if (face.has_neighbor) continue;
const size_t num_face_nodes = face.vertex_ids.size();
for (size_t fi=0; fi<num_face_nodes; ++fi)
{
const uint i = cell_mapping.MapFaceNode(f,fi);
node_boundary_flag[i] = true;
}
}
Notice the use of face.has_neighbor here. If the face does not have a neighbor it means the face is on a boundary and therefore a Dirichlet node. Once this condition applies we loop over the face nodes, map the face-node to a cell-node then flag that node as being on a boundary.
Finally, we now assemble the local cell-matrix and local RHS into the global system.
for (size_t i=0; i<num_nodes; ++i)
{
if (node_boundary_flag[i])
{
MatSetValue(A, imap[i], imap[i], 1.0, ADD_VALUES);
VecSetValue(b, imap[i], 0.0, ADD_VALUES);
}
else
{
for (size_t j=0; j<num_nodes; ++j)
{
if (not node_boundary_flag[j])
MatSetValue(A, imap[i], imap[j], Acell[i][j], ADD_VALUES);
}
VecSetValue(b, imap[i], cell_rhs[i], ADD_VALUES);
}
}
We essentially loop over each node, after which we have two conditions: if the node is a boundary node then we just add an entry on the diagonal, if the node is not a boundary node we then loop over the row entries. We perform a check again to see if the j-entries are boundary nodes. If they are we put them on the RHS, if they are not then they are allowed to be matrix entries.
After this process we assemble the matrix and the RHS globally like we did before:
chi::log.Log() << "Global assembly";
MatAssemblyBegin(A, MAT_FINAL_ASSEMBLY);
MatAssemblyEnd(A, MAT_FINAL_ASSEMBLY);
VecAssemblyBegin(b);
VecAssemblyEnd(b);
chi::log.Log() << "Done global assembly";
6 Solving and visualizing
Solving the system and visualizing it is the same as was done for the Finite Volume tutorial. The matrix is still Symmetric Positive Definite (SPD) so we use the same solver/precondtioner setup.
chi::log.Log() << "Solving: ";
auto petsc_solver =
A,
"PWLCDiffSolver",
KSPCG,
PCGAMG,
1.0e-6,
1000);
KSPSolve(petsc_solver.ksp,b,x);
chi::log.Log() << "Done solving";
std::vector<double> field;
sdm.LocalizePETScVector(x,field,OneDofPerNode);
KSPDestroy(&petsc_solver.ksp);
VecDestroy(&x);
VecDestroy(&b);
MatDestroy(&A);
chi::log.Log() << "Done cleanup";
auto ff = std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
);
ff->UpdateFieldVector(field);
ff->ExportToVTK("CodeTut3_PWLC");
PETScSolverSetup CreateCommonKrylovSolverSetup(Mat ref_matrix, const std::string &in_solver_name="KSPSolver", const std::string &in_solver_type=KSPGMRES, const std::string &in_preconditioner_type=PCNONE, double in_relative_residual_tolerance=1.0e-6, int64_t in_maximum_iterations=100)
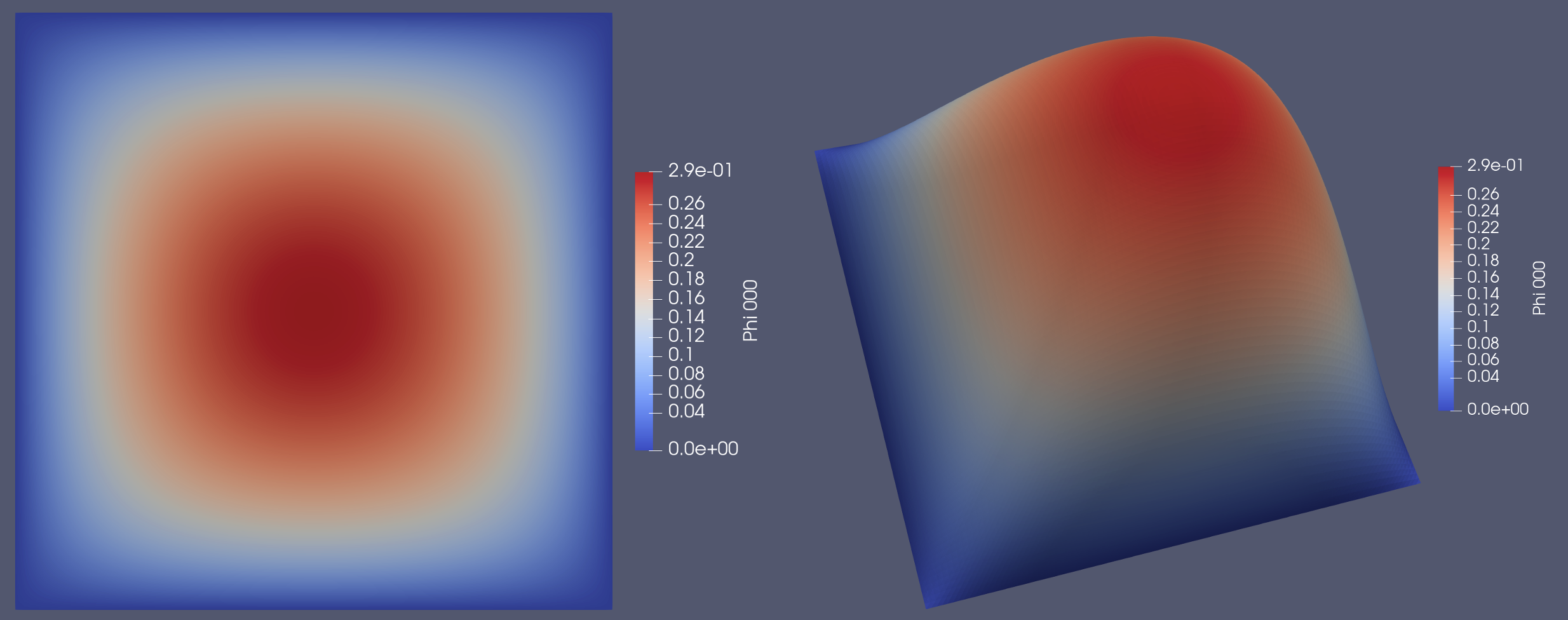
Solution for a 2D mesh with a flat and warped view
The complete program
#include "math/SpatialDiscretization/FiniteElement/PiecewiseLinear/pwlc.h"
#include "physics/FieldFunction/fieldfunction2.h"
int main(
int argc,
char* argv[])
{
chi::Initialize(argc,argv);
chi::RunBatch(argc, argv);
chi::log.Log() << "Coding Tutorial 3";
const auto& grid = *grid_ptr;
chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_PWLC::New(grid_ptr);
const auto& sdm = *sdm_ptr;
const auto& OneDofPerNode = sdm.UNITARY_UNKNOWN_MANAGER;
const size_t num_local_dofs = sdm.GetNumLocalDOFs(OneDofPerNode);
const size_t num_globl_dofs = sdm.GetNumGlobalDOFs(OneDofPerNode);
chi::log.Log() << "Num local DOFs: " << num_local_dofs;
chi::log.Log() << "Num globl DOFs: " << num_globl_dofs;
const auto n = static_cast<int64_t>(num_local_dofs);
const auto N = static_cast<int64_t>(num_globl_dofs);
std::vector<int64_t> nodal_nnz_in_diag;
std::vector<int64_t> nodal_nnz_off_diag;
sdm.BuildSparsityPattern(nodal_nnz_in_diag,nodal_nnz_off_diag, OneDofPerNode);
nodal_nnz_in_diag,
nodal_nnz_off_diag);
chi::log.Log() << "Assembling system: ";
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto qp_data = cell_mapping.MakeVolumeQuadraturePointData();
const size_t num_nodes = cell_mapping.NumNodes();
VecDbl cell_rhs(num_nodes, 0.0);
for (size_t i=0; i<num_nodes; ++i)
{
for (size_t j=0; j<num_nodes; ++j)
{
double entry_aij = 0.0;
for (size_t qp : qp_data.QuadraturePointIndices())
{
entry_aij +=
qp_data.ShapeGrad(i, qp).Dot(qp_data.ShapeGrad(j, qp)) *
qp_data.JxW(qp);
}
Acell[i][j] = entry_aij;
}
for (size_t qp : qp_data.QuadraturePointIndices())
cell_rhs[i] += 1.0 * qp_data.ShapeValue(i, qp) * qp_data.JxW(qp);
}
std::vector<bool> node_boundary_flag(num_nodes, false);
const size_t num_faces = cell.faces.size();
for (size_t f=0; f<num_faces; ++f)
{
const auto& face = cell.faces[f];
if (face.has_neighbor) continue;
const size_t num_face_nodes = face.vertex_ids.size();
for (size_t fi=0; fi<num_face_nodes; ++fi)
{
const uint i = cell_mapping.MapFaceNode(f,fi);
node_boundary_flag[i] = true;
}
}
std::vector<int64_t> imap(num_nodes, 0);
for (size_t i=0; i<num_nodes; ++i)
imap[i] = sdm.MapDOF(cell, i);
for (size_t i=0; i<num_nodes; ++i)
{
if (node_boundary_flag[i])
{
MatSetValue(A, imap[i], imap[i], 1.0, ADD_VALUES);
VecSetValue(b, imap[i], 0.0, ADD_VALUES);
}
else
{
for (size_t j=0; j<num_nodes; ++j)
{
if (not node_boundary_flag[j])
MatSetValue(A, imap[i], imap[j], Acell[i][j], ADD_VALUES);
}
VecSetValue(b, imap[i], cell_rhs[i], ADD_VALUES);
}
}
}
chi::log.Log() << "Global assembly";
MatAssemblyBegin(A, MAT_FINAL_ASSEMBLY);
MatAssemblyEnd(A, MAT_FINAL_ASSEMBLY);
VecAssemblyBegin(b);
VecAssemblyEnd(b);
chi::log.Log() << "Done global assembly";
chi::log.Log() << "Solving: ";
auto petsc_solver =
A,
"PWLCDiffSolver",
KSPCG,
PCGAMG,
1.0e-6,
1000);
KSPSolve(petsc_solver.ksp,b,x);
chi::log.Log() << "Done solving";
std::vector<double> field;
sdm.LocalizePETScVector(x,field,OneDofPerNode);
KSPDestroy(&petsc_solver.ksp);
VecDestroy(&x);
VecDestroy(&b);
MatDestroy(&A);
chi::log.Log() << "Done cleanup";
auto ff = std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
);
ff->UpdateFieldVector(field);
ff->ExportToVTK("CodeTut3_PWLC");
chi::Finalize();
return 0;
}


![]() ,
, ![]()
![]() denotes the divergence-operator and
denotes the divergence-operator and ![]() denotes the gradient-operator, i.e.
denotes the gradient-operator, i.e. ![]() denotes the gradient of
denotes the gradient of ![]() . The boundary conditions here state that
. The boundary conditions here state that ![]() on the boundary.
on the boundary.![]() and
and ![]() a cartesian domain, either 1D, 2D or 3D, with each dimension always between
a cartesian domain, either 1D, 2D or 3D, with each dimension always between ![]() . We can generate the mesh for this problem using an input file
. We can generate the mesh for this problem using an input file 
![]() , where
, where ![]() is a unique node in the problem, and then integrate over the volume of the domain
is a unique node in the problem, and then integrate over the volume of the domain ![]()
![]()
![]()
![]()
![]() using essentially a very fancy interpolation scheme. With this scheme we approximate
using essentially a very fancy interpolation scheme. With this scheme we approximate ![]() as
as ![]() where
where ![]()
![]() do not dependent on space and
do not dependent on space and ![]() are called shape functions. For this tutorial we will be utilizing the Piecewise Linear Continuous (PWLC) shape functions which are generally specially in the fact that they can support arbitrary polygons and polyhedra.
are called shape functions. For this tutorial we will be utilizing the Piecewise Linear Continuous (PWLC) shape functions which are generally specially in the fact that they can support arbitrary polygons and polyhedra.![]() being the same as the shape functions, i.e.,
being the same as the shape functions, i.e., ![]() .
.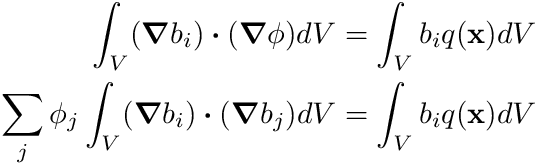
![]() are defined cell-by-cell, therefore we can drill a little deeper by defining
are defined cell-by-cell, therefore we can drill a little deeper by defining ![]()
![]() is the volume of cell
is the volume of cell ![]() . The function
. The function ![]() is a function uniquely defined within cell
is a function uniquely defined within cell ![]() 's volume.
's volume.![]()
![]() is position in the reference coordinate frame,
is position in the reference coordinate frame, ![]() is the magnitude of the Jacobian,
is the magnitude of the Jacobian, ![]() is the volume of the reference element, and
is the volume of the reference element, and ![]() is the reference element equivalent of
is the reference element equivalent of ![]() . Now, the big advantage of doing this is that we can use quadrature rules for these integrals
. Now, the big advantage of doing this is that we can use quadrature rules for these integrals ![]()
![]() are the abscissas of the quadrature rule and
are the abscissas of the quadrature rule and ![]() are the quadrature weights.
are the quadrature weights.![]()
![]()
![]() node combinations of our equation above but with scope only on the local element. Notice that we never actually pass around the actual quadrature points but rather use the quadrature point indices via
node combinations of our equation above but with scope only on the local element. Notice that we never actually pass around the actual quadrature points but rather use the quadrature point indices via ![]()
![]() , where
, where ![]() is combined into
is combined into ![]() essentially becomes
essentially becomes ![]() for our case of zero Dirichlet boundary conditions. This essentially places just a 1 on the diagonal with no entries off-diagonal for the entire row
for our case of zero Dirichlet boundary conditions. This essentially places just a 1 on the diagonal with no entries off-diagonal for the entire row ![]() . Therefore, we need to modify the local cell-matrix to reflect this situation.
. Therefore, we need to modify the local cell-matrix to reflect this situation.![]() will need to be moved to the RHS. This is because it could destroy the symmetry of an otherwise symmetric matrix.
will need to be moved to the RHS. This is because it could destroy the symmetry of an otherwise symmetric matrix.