Table of Contents
1 Introduction
Monte Carlo based flux estimators traditionally use a number of tracks, traced within a volume, to estimate the scalar flux. For 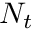 amount of tracks traced inside a volume,
amount of tracks traced inside a volume, 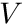 , originating from a sample of
, originating from a sample of 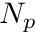 number of particles/rays, the scalar flux,
number of particles/rays, the scalar flux, 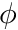 , can be estimated with
, can be estimated with
![\[ \phi \approx \frac{1}{N_p V} \sum_t^{N_t} \ell_t, \]](../../form_242.png)
where 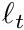 is the
is the 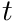 -th track length. This simply means that the scalar flux is the "average track length per unit volume".
-th track length. This simply means that the scalar flux is the "average track length per unit volume".
The individual tracks of these particles can be assigned a weight, 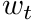 , enabling a multitude of features.
, enabling a multitude of features.
![\[ \phi \approx \frac{1}{N_p V} \sum_t^{N_t} \ell_t w_t, \]](../../form_246.png)
For our purposes we are interested in three possible weightings, i) weighting by a spherical harmonic, which can be used to compute flux moments, ii) weighting by average FE shape function values, allowing the projection of flux onto a FE space, and finally iii) weighting with an exponential attenuation, allowing the computation of uncollided flux.
1.1 Weighting with a spherical harmonic
Applying a weight with a spherical harmonic is conceptually simple. For the 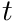 -th track we simply set the weight to the spherical harmonic evaluated with the direction,
-th track we simply set the weight to the spherical harmonic evaluated with the direction, 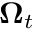 , of the track,
, of the track,
![\[ \phi_{\ell m} \approx \frac{1}{N_p V} \sum_t^{N_t} \ell_t Y_{\ell m}( \boldsymbol{\Omega}_t), \]](../../form_248.png)
1.2 Weighting by average FE shape function values
For a DFEM projection of the fluxes we require nodal values, on each cell, for a given flux quantity, 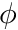 . Therefore we seek
. Therefore we seek 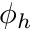 such that
such that
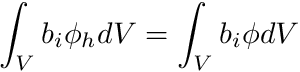
and since 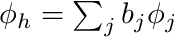 we need to solve the cell-by-cell system defined by
we need to solve the cell-by-cell system defined by
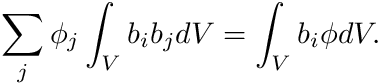
In this system the entries 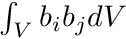 are simply the entries of the mass matrix,
are simply the entries of the mass matrix, 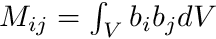 , and we still need to find the rhs-entries
, and we still need to find the rhs-entries 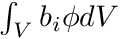 . This is where we will use the track length based estimators by weighting with the shape functions b_i.
. This is where we will use the track length based estimators by weighting with the shape functions b_i.
In this formulation we have
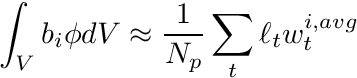
where
![\[ w_t^{i,avg} = \frac{ \int_{s_a}^{s_b} b_i(s\mapsto \mathbf{x}) ds } {\int_{s_a}^{s_b} ds} = \frac{ \int_{s_a}^{s_b} b_i(s\mapsto \mathbf{x}) ds } {\ell_t}, \]](../../form_257.png)
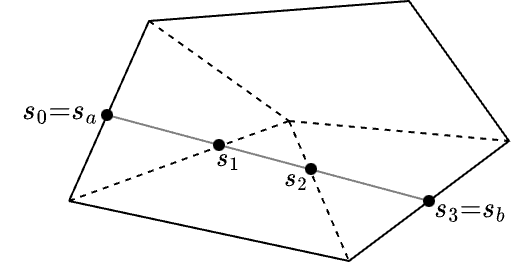
the average basis function value along the track. For ordinary Lagrange FE shape functions, which are not defined piecewise, the integral in the numerator can be obtained exactly using a numerical quadrature. For our applications, where we use the PWLD FE shape functions we need to split this integral per segment of the basic cell crossed.
For example, consider the polygon below, where a ray is traced from position 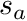 to
to 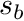 .
.
The track traced across the cell needs to be split into the segments defined by the sub-triangles of the polygon it crossed (for polyhedrons this would be the sub-tetrahedrons). Therefore the track 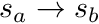 needs to be split into tracks
needs to be split into tracks 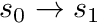 ,
, 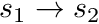 and
and 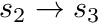 as per the figure. Therefore the integral becomes
as per the figure. Therefore the integral becomes
![\[ \int_{s_a}^{s_b} b_i(s\mapsto \mathbf{x}) ds = \int_{s_0}^{s_1} b_i(s\mapsto \mathbf{x}) ds + \int_{s_1}^{s_2} b_i(s\mapsto \mathbf{x}) ds + \int_{s_2}^{s_3} b_i(s\mapsto \mathbf{x}) ds \]](../../form_264.png)
which we can evaluate analytically since it is linear on each segment.
Note: The mapping of 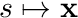 can be quite expensive so in this particular case it would be better to evaluate the shape function at the half-way point of each segment, after which the integral becomes
can be quite expensive so in this particular case it would be better to evaluate the shape function at the half-way point of each segment, after which the integral becomes
![\[ \int_{s_a}^{s_b} b_i(s\mapsto \mathbf{x}) ds = b_i(\frac{s_0 + s_1}{2}\mapsto \mathbf{x}) (s_1 - s_0) + b_i(\frac{s_1 + s_2}{2}\mapsto \mathbf{x}) (s_2 - s_1) + b_i(\frac{s_2 + s_3}{2}\mapsto \mathbf{x}) (s_3 - s_2) + \]](../../form_266.png)
1.3 Weighting with an exponential attenuation
Weighting with an exponential attenuation adds the final piece of weighting necessary to efficiently compute the uncollided flux.
The exponential attenuation of the uncollided flux, 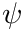 , along the path of a ray with direction
, along the path of a ray with direction  is expressed as
is expressed as
![\[ \frac{d\psi}{ds} = -\sigma_t(s) \psi(s) \]](../../form_268.png)
where 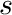 is the distance traveled and
is the distance traveled and 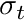 is the total cross section. From this model we can compute the attenuation across a cell, with constant
is the total cross section. From this model we can compute the attenuation across a cell, with constant 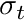 , as
, as
![\[ \psi(s) = \psi(s=0) e^{-\sigma_t s} \]](../../form_271.png)
where 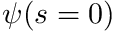 is the value of
is the value of 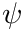 when it entered the cell.
when it entered the cell.
To assimilate all of this into a raytracing algorithm we start a source particle with a weight, 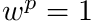 , which acts as the proxy for
, which acts as the proxy for 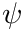 (i.e.,
(i.e., 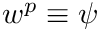 ). From this we can determine the nodal uncollided flux,
). From this we can determine the nodal uncollided flux, 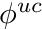 , in a similar fashion as we would determine the regular flux, i.e.,
, in a similar fashion as we would determine the regular flux, i.e.,
![\[ \sum_j \phi_j^{uc} \int_V b_i b_j dV = \int_V b_i \phi^{uc} dV, \]](../../form_276.png)
however, now we need additional treatment for the integral containing 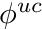 , for which we have
, for which we have
![\[ \int_V b_i \phi^{uc} dV \approx \frac{1}{N_p} \sum_t \ell_t w_t^{i,avg}, \]](../../form_277.png)
where, this time,
![\[ w_t^{i,avg} = \frac{ \int_{s_a}^{s_b} w^p(s) b_i(s\mapsto \mathbf{x}) ds } {\ell_t}. \]](../../form_278.png)
Note here that 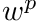 is a function of position, specifically
is a function of position, specifically
![\[ w^p(s) = w^p(s=s_a) e^{-\sigma_t s} \]](../../form_280.png)
and so is the basis function 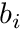 .
.
The form of this integral needs to split into segments in the same way we did in the previous subsection. Therefore, given K amount of segments, we now have
![\[ \ell_t w_t^{i,avg} = \sum_{k=0}^{K-1} \ell_{tk} w_{tk}^{i,avg} \]](../../form_282.png)
where 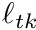 is the track length of the
is the track length of the 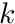 -th segment and
-th segment and 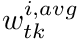 is the average weight of this segment. The weight is computed with
is the average weight of this segment. The weight is computed with
![\[ w_{tk}^{i,avg} = \frac{ \int_{s_k}^{s_{k+1}} w^p(s) b_i(s\mapsto \mathbf{x}) ds } {\ell_{tk}}. \]](../../form_286.png)
where 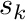 and
and 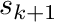 are the beginning and ending positions of segment
are the beginning and ending positions of segment 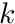 respectively.
respectively.
Note here that, since we have an expression for 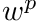 , we can compute
, we can compute 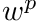 at any point along track
at any point along track 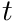 including at the start of any segment. Therefore we define
including at the start of any segment. Therefore we define 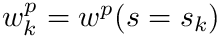 which allows us to express
which allows us to express 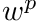 as
as
![\[ w^p(s) = w_k^p e^{-\sigma_t(s-s_k)}, \quad \quad \quad s\in[s_k,s_{k+1}] \]](../../form_290.png)
Additionally we express the basis functions on a segment, since we know the shape function is linear on the segment, as
![\[ b_i(s) = b_{i,k} \frac{s_{k+1}-s}{s_{k+1}-s_k} + b_{i,k+1} \frac{s-s_k}{s_{k+1}-s_k} \]](../../form_291.png)
where 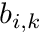 and
and 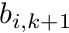 are the basis function values at the beginning and end of the segment, respectively. These two expressions allow us to evaluate the segment average weight as
are the basis function values at the beginning and end of the segment, respectively. These two expressions allow us to evaluate the segment average weight as
![\[ w_{tk}^{i,avg} = \frac{1}{\ell_{tk}} \int_{s_k}^{s_{k+1}} w_k^p e^{-\sigma_t(s-s_k)} \biggr[ b_{i,k} \frac{s_{k+1}-s}{s_{k+1}-s_k} + b_{i,k+1} \frac{s-s_k}{s_{k+1}-s_k} \biggr] ds \]](../../form_294.png)
and since 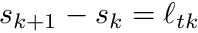 we can simplify this expression as
we can simplify this expression as
![\begin{align*} w_{tk}^{i,avg} &= \frac{1}{\ell_{tk}} \int_{0}^{\ell_{tk}} w_k^p e^{-\sigma_t s' } \biggr[ b_{i,k} \frac{\ell_{tk}-s'}{\ell_{tk}} + b_{i,k+1} \frac{s'}{\ell_{tk}} \biggr] ds' \\ &= \frac{1}{\ell_{tk}^2} \int_{0}^{\ell_{tk}} w_k^p e^{-\sigma_t s' } \biggr[ b_{i,k} \ell_{tk} + (b_{i,k+1} - b_{i,k} ) s' \biggr] ds' \end{align*}](../../form_296.png)
which is in the general form
![\[ w_{tk}^{i,avg} = \frac{w_k^p}{\ell_{tk}^2} \int_{0}^{\ell_{tk}} e^{-\sigma_t s'} \biggr[ C_0 + C_1 s' \biggr] ds' \]](../../form_297.png)
where
![\[ C_0 = b_{i,k} \ell_{tk} \]](../../form_298.png)
![\[ C_1 = b_{i,k+1} - b_{i,k}. \]](../../form_299.png)
With these constants defined the expression can be evaluated analytically
![\[ w_{tk}^{i,avg} = \frac{w_k^p}{\ell_{tk}^2} \biggr[ \frac{C_0}{\sigma_t} (1-e^{-\sigma_t \ell_{tk}}) + \frac{C_1}{\sigma_t^2} \biggr( 1 - (1 + \sigma_t \ell_{tk} ) \biggr)e^{-\sigma_t \ell_{tk}} \biggr] \]](../../form_300.png)
2 Program setup
We start by getting the grid as usual:
const auto& grid = *grid_ptr;
chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
chi_mesh::MeshContinuumPtr & GetGrid() const
MeshHandler & GetCurrentHandler()
Note here that we grab the dimension.
Next we set a number of parameters important to the simulation:
const size_t num_groups = 1;
const size_t scattering_order = 1;
const auto& L = scattering_order;
const size_t num_moments =
(dimension == 1)? L + 1 :
(dimension == 2)? (L+1)*(L+2)/2 :
(dimension == 3)? (L+1)*(L+1) : 0;
const double sigma_t = 0.27;
std::vector<std::pair<int,int>> m_to_ell_em_map;
if (dimension == 1)
for (int ell=0; ell<=scattering_order; ell++)
m_to_ell_em_map.emplace_back(ell,0);
else if (dimension == 2)
for (int ell=0; ell<=scattering_order; ell++)
for (int m=-ell; m<=ell; m+=2)
m_to_ell_em_map.emplace_back(ell,m);
else if (dimension == 3)
for (int ell=0; ell<=scattering_order; ell++)
for (int m=-ell; m<=ell; m++)
m_to_ell_em_map.emplace_back(ell,m);
The interesting items here includes the scattering_order and the map from linear moment index to harmonic indices, m_to_ell_em_map. See the LBS Whitepaper for the detail of this but in a nutshell... Only some of the harmonics are relevant in certain dimensions.
Next we build the spatial discretization, which in this case would be a PWLD discretization, and we do this as normal:
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_PWLD::New(grid_ptr);
const auto& sdm = *sdm_ptr;
std::shared_ptr< SpatialDiscretization > SDMPtr
For the unknown manager and DOF-counts we build an unknown manager as follows:
for (size_t m=0; m<num_moments; ++m)
unsigned int AddUnknown(UnknownType unk_type, unsigned int dimension=0)
And then grab the dof-counts
const size_t num_fem_local_dofs = sdm.GetNumLocalDOFs(phi_uk_man);
const size_t num_fem_globl_dofs = sdm.GetNumGlobalDOFs(phi_uk_man);
chi::log.Log() << "Num local FEM DOFs: " << num_fem_local_dofs;
chi::log.Log() << "Num globl FEM DOFs: " << num_fem_globl_dofs;
This allows us to define the business end, which is the flux tally vector:
std::vector<double> phi_tally(num_fem_local_dofs, 0.0);
3 The particle/ray data structure
The particle/ray data structure is the packet of data that we will be sending around in our ray tracing algorithm. First we need the basic structure:
struct Particle
{
Vec3 position = {0.0,0.0,0.0};
Vec3 direction = {0.0,0.0,0.0};
int energy_group = 0;
double weight = 1.0;
uint64_t cell_id = 0;
bool alive = true;
};
This is all basic stuff. Essentially the particle's state is tracked with the members position, direction, energy_group and weight. The other two members are simply auxiliary items to assist with the transport process.
Next we define a source, along with the determining which cell contains the source:
const Vec3 source_pos = {0.0,0.0,0.0};
for (auto& cell : grid.local_cells)
if (grid.CheckPointInsideCell(cell, source_pos))
{
source_cell_ptr = &cell;
break;
}
if (source_cell_ptr == nullptr)
throw std::logic_error(fname + ": Source cell not found.");
const uint64_t source_cell_id = source_cell_ptr->global_id;
Notice here we used the grid utility CheckPointInsideCell.
4 Utility lambdas
In this section we define 3 utility functions in the form of c++ lambdas. i) A routine to sample a random direction. This gets used when we sample the source. ii) A routine to contribute a track to a PWLD tally. This is very complicated and will be explained. iii) A routine to approximate a given cell's size. The approximate cell sizes are used by the raytracer (which we will discuss later) to set appropriate tolerances used during the sub-routines of the raytracer.
4.1 Sampling a random direction
Given a random number generator we can use two random numbers to sample the azimuthal- and polar directions. The azimuthal angle is sampled uniformly, i.e., ![$ \varphi \in [0,2\pi] $](../../form_301.png) whilst the polar angle is determined by sampling the cosine of the polar angle uniformly, i.e.,
whilst the polar angle is determined by sampling the cosine of the polar angle uniformly, i.e., ![$ \cos \theta = \mu \in [-1,1] $](../../form_302.png) .
.
auto SampleRandomDirection = [&rng]()
{
double costheta = 2.0*rng.
Rand() - 1.0;
double theta = acos(costheta);
double varphi = rng.
Rand()*2.0*M_PI;
sin(theta) * sin(varphi),
cos(theta)};
};
It is important to note that one should only use a single random number, which, gets reused, and not define new ones since the random seed for new generators will be the same.
4.2 PWLD Tally contribution
The tally contribution routine takes a track, defined by a starting and ending position, and contributes it to the specified cell's tally information. Of course additional information about the particle creating the track is also provided, i.e., the direction, energy group index and weight at the starting position.
auto ContributePWLDTally = [&sdm,&grid,&phi_tally,&phi_uk_man,&sigma_t,
&num_moments,&m_to_ell_em_map](
const Vec3& positionA,
const Vec3& positionB,
const Vec3& omega,
const int g,
double weight)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const size_t num_nodes = cell_mapping.NumNodes();
const double phi = phi_theta.first;
const double theta = phi_theta.second;
std::vector<double> segment_lengths;
cell,
positionA,
positionB,
omega,
segment_lengths);
std::vector<double> shape_values_k;
std::vector<double> shape_values_kp1;
cell_mapping.ShapeValues(positionA,
shape_values_k);
double d_run_sum = 0.0;
for (const auto& segment_length_k : segment_lengths)
{
d_run_sum += segment_length_k;
const double& d = d_run_sum;
cell_mapping.ShapeValues(positionA+omega*d, shape_values_kp1);
const auto& b_ik = shape_values_k;
const auto& b_ikp1 = shape_values_kp1;
const double& ell_k = segment_length_k;
for (size_t i=0; i<num_nodes; ++i)
{
const double C0 = b_ik[i] * ell_k;
const double C1 = b_ikp1[i] - b_ik[i];
for (size_t m=0; m < num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
const auto& ell_em = m_to_ell_em_map.at(m);
const int ell = ell_em.first;
const int em = ell_em.second;
double w_exp = (C0 / sigma_t) * (1.0 - exp(-sigma_t * ell_k)) +
(C1 / (sigma_t * sigma_t)) *
(1.0 - (1 + sigma_t * ell_k) * exp(-sigma_t * ell_k));
w_exp *= weight / (ell_k * ell_k);
double w_avg = w_harmonic * w_exp;
phi_tally[dof_map] += ell_k * w_avg ;
}
}
shape_values_k = shape_values_kp1;
weight *= exp(-sigma_t * segment_length_k);
}
};
std::pair< double, double > OmegaToPhiThetaSafe(const chi_mesh::Vector3 &omega)
double Ylm(unsigned int ell, int m, double varphi, double theta)
void PopulateRaySegmentLengths(const chi_mesh::MeshContinuum &grid, const Cell &cell, const chi_mesh::Vector3 &line_point0, const chi_mesh::Vector3 &line_point1, const chi_mesh::Vector3 &omega, std::vector< double > &segment_lengths)
The first portion of this routine is just housekeeping,
const auto& cell_mapping = sdm.GetCellMapping(cell);
const size_t num_nodes = cell_mapping.NumNodes();
const double phi = phi_theta.first;
const double theta = phi_theta.second;
We get the cell mapping, number of nodes, and we convert the direction vector to a 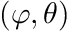 pair. The latter will be used for the harmonic weighting.
pair. The latter will be used for the harmonic weighting.
Next we determing the segments crossed by this track. This information is populated into a vector of segment lengths, sorted according to the direction traveled by the ray, by using the routine chi_mesh::PopulateRaySegmentLengths().
std::vector<double> segment_lengths;
cell,
positionA,
positionB,
omega,
segment_lengths);
We then declare two vectors that will hold the shape function values at different places on the segments. We can immediately determine the shape values at  since this will be at position A.
since this will be at position A.
std::vector<double> shape_values_k;
std::vector<double> shape_values_kp1;
cell_mapping.ShapeValues(positionA,
shape_values_k);
Next we start looping over the segments.
double d_run_sum = 0.0;
for (const auto& segment_length_k : segment_lengths)
{
d_run_sum += segment_length_k;
const double& d = d_run_sum;
cell_mapping.ShapeValues(positionA+omega*d, shape_values_kp1);
const auto& b_ik = shape_values_k;
const auto& b_ikp1 = shape_values_kp1;
const double& ell_k = segment_length_k;
We determine the end position of the segment using a running sum of the total segments traversed. We then populate the shape function values at 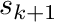 and rename both sets of shape function values and the segment length for convenience.
and rename both sets of shape function values and the segment length for convenience.
Next we loop over the nodes and moments.
for (size_t i=0; i<num_nodes; ++i)
{
const double C0 = b_ik[i] * ell_k;
const double C1 = b_ikp1[i] - b_ik[i];
for (size_t m=0; m < num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
Once a node is identified we compute the constants C0 and C1. Also once in the moment loop we can obtain the DOF local index of the tally.
Next we compute the harmonic weighting:
const auto& ell_em = m_to_ell_em_map.at(m);
const int ell = ell_em.first;
const int em = ell_em.second;
Then we compute the exponential weighting based on the formula
![\[ w_{tk}^{i,avg} = \frac{w_k^p}{\ell_{tk}^2} \biggr[ \frac{C_0}{\sigma_t} (1-e^{-\sigma_t \ell_{tk}}) + \frac{C_1}{\sigma_t^2} \biggr( 1 - (1 + \sigma_t \ell_{tk} ) \biggr)e^{-\sigma_t \ell_{tk}} \biggr] \]](../../form_300.png)
with the code
double w_exp = (C0 / sigma_t) * (1.0 - exp(-sigma_t * ell_k)) +
(C1 / (sigma_t * sigma_t)) *
(1.0 - (1 + sigma_t * ell_k) * exp(-sigma_t * ell_k));
w_exp *= weight / (ell_k * ell_k);
Finally, the average weight is computed and the tally contribution is made
double w_avg = w_harmonic * w_exp;
phi_tally[dof_map] += ell_k * w_avg ;
At the end of each segment being processed we copy the shape function values at 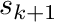 to
to 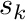 , preventing us from having to compute the values at
, preventing us from having to compute the values at 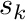 again (which can be expensive). We also apply the exponential attenuation to the particle weight over the segment.
again (which can be expensive). We also apply the exponential attenuation to the particle weight over the segment.
shape_values_k = shape_values_kp1;
weight *= exp(-sigma_t * segment_length_k);
4.3 Approximating cell size
To obtain a very rough estimate of a cell's size we simply determine its bounding box:
{
const auto& v0 = grid.vertices[cell.vertex_ids[0]];
double xmin = v0.x, xmax = v0.x;
double ymin = v0.y, ymax = v0.y;
double zmin = v0.z, zmax = v0.z;
for (uint64_t vid : cell.vertex_ids)
{
const auto& v = grid.vertices[vid];
xmin = std::min(xmin, v.x); xmax = std::max(xmax, v.x);
ymin = std::min(ymin, v.y); ymax = std::max(ymax, v.y);
zmin = std::min(zmin, v.z); zmax = std::max(zmax, v.z);
}
};
The code here should be self explanatory.
5 The raytracer
Instantiating a chi_mesh::RayTracer object is very simple. It just needs the grid and the approximate cell sizes.
std::vector<double> cell_sizes(grid.local_cells.size(), 0.0);
for (const auto& cell : grid.local_cells)
cell_sizes[cell.local_id] = GetCellApproximateSize(cell);
6 Executing the algorithms
The basic process of simulating all the rays is fairly simple
const size_t num_particles = 10'000'000;
for (size_t n=0; n<num_particles; ++n)
{
if (n % size_t(num_particles/10.0) == 0)
std::cout << "#particles = " << n << "\n";
const auto omega = SampleRandomDirection();
Particle particle{source_pos,
omega,
0,
1.0,
source_cell_id,
true};
while (particle.alive)
{
const auto& cell = grid.cells[particle.cell_id];
auto destination_info = ray_tracer.TraceRay(cell,
particle.position,
particle.direction);
const Vec3& end_of_track_position = destination_info.pos_f;
const int g = particle.energy_group;
if (sdm.type == PWLD)
ContributePWLDTally(cell,
particle.position,
end_of_track_position,
particle.direction,
g,
particle.weight);
if (not destination_info.particle_lost)
{
const auto& f = destination_info.destination_face_index;
const auto& current_cell_face = cell.faces[f];
if (current_cell_face.has_neighbor)
particle.cell_id = current_cell_face.neighbor_id;
else
particle.alive = false;
}
else
{
std::cout << "particle" << n << " lost "
<< particle.position.PrintStr() << " "
<< particle.direction.PrintStr() << " "
<< "\n";
break;
}
const auto& pA = particle.position;
const auto& pB = end_of_track_position;
particle.weight *= exp(-sigma_t*(pB-pA).Norm());
particle.position = end_of_track_position;
}
}
We start the process with the loop
const size_t num_particles = 10'000'000;
for (size_t n=0; n<num_particles; ++n)
{
if (n % size_t(num_particles/10.0) == 0)
std::cout << "#particles = " << n << "\n";
The information printing line simply prints at each 10% of completion.
We then create a source particle/ray
const auto omega = SampleRandomDirection();
Particle particle{source_pos,
omega,
0,
1.0,
source_cell_id,
true};
Next we keep transporting the particle as long as it is alive. The beginning of this loop is
while (particle.alive)
{
const auto& cell = grid.cells[particle.cell_id];
auto destination_info = ray_tracer.TraceRay(cell,
particle.position,
particle.direction);
const Vec3& end_of_track_position = destination_info.pos_f;
After a trace we have one single track within a cell.
We then contribute the PWLD tally
ContributePWLDTally(cell,
particle.position,
end_of_track_position,
particle.direction,
particle.energy_group,
particle.weight);
Next we process the transfer of the particle to the next cell. If the particle hit a cell face without a neighbor then the particle is killed (i.e., alive set to false. Under some circumstances the raytracer could also fail, resulting in a lost particle, for which we print a verbose message.
if (not destination_info.particle_lost)
{
const auto& f = destination_info.destination_face_index;
const auto& current_cell_face = cell.faces[f];
if (current_cell_face.has_neighbor)
particle.cell_id = current_cell_face.neighbor_id;
else
particle.alive = false;
}
else
{
std::cout << "particle" << n << " lost "
<< particle.position.PrintStr() << " "
<< particle.direction.PrintStr() << " "
<< "\n";
break;
}
Lastly we update the particle's attenuation and position
const auto& pA = particle.position;
const auto& pB = end_of_track_position;
particle.weight *= exp(-sigma_t*(pB-pA).Norm());
particle.position = end_of_track_position;
7 Post-processing the tallies
The tallies up to this point are still in raw format. We need to convert them to the project fashion we want.
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& qp_data = cell_mapping.MakeVolumeQuadraturePointData();
const size_t num_nodes = cell_mapping.NumNodes();
for (auto qp : qp_data.QuadraturePointIndices())
for (size_t i=0; i<num_nodes; ++i)
for (size_t j=0; j<num_nodes; ++j)
M[i][j] += qp_data.ShapeValue(i,qp) * qp_data.ShapeValue(j, qp) *
qp_data.JxW(qp);
for (size_t m=0; m<num_moments; ++m)
for (size_t g=0; g<num_groups; ++g)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
b[i] = phi_tally[imap] / num_particles;
}
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
phi_tally[imap] = c[i];
}
}
}
std::vector< VecDbl > MatDbl
std::vector< double > VecDbl
MatDbl Inverse(const MatDbl &A)
MatDbl MatMul(const MatDbl &A, const double c)
The first portion of the loop is simply housekeeping again
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& qp_data = cell_mapping.MakeVolumeQuadraturePointData();
const size_t num_nodes = cell_mapping.NumNodes();
for (auto qp : qp_data.QuadraturePointIndices())
for (size_t i=0; i<num_nodes; ++i)
for (size_t j=0; j<num_nodes; ++j)
M[i][j] += qp_data.ShapeValue(i,qp) * qp_data.ShapeValue(j, qp) *
qp_data.JxW(qp);
We get the cell mapping, quadrature point data, and we build the mass matrix. Recall that we need 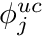 such that
such that
![\[ \sum_j \phi_j^{uc} \int_V b_i b_j dV = \int_V b_i \phi^{uc} dV, \]](../../form_276.png)
which requires us to solve the small system
![\[ M \boldsymbol{\phi}^{uc} = \mathbf{T} \]](../../form_306.png)
where 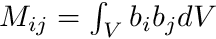 and
and 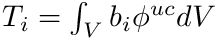 . Since the mass matrix is such a small matrix we just directly invert it to be used for all groups and moments.
. Since the mass matrix is such a small matrix we just directly invert it to be used for all groups and moments.
Next we loop over all moments and groups.
for (size_t m=0; m<num_moments; ++m)
for (size_t g=0; g<num_groups; ++g)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
T[i] = phi_tally[imap] / num_particles;
}
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
phi_tally[imap] = phi_uc[i];
}
}
Within the moment and group loop we first set the entries of 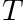 to the normalized tally values. Thereafter we multiply
to the normalized tally values. Thereafter we multiply 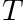 from the left with
from the left with 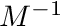 to get
to get 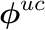 . Finally we reuse the tally data and set the nodal values of the tally to the uncollided projected flux.
. Finally we reuse the tally data and set the nodal values of the tally to the uncollided projected flux.
8 Exporting field functions
Creating the field functions is similar to what we did in previous tutorials
std::vector<std::shared_ptr<chi_physics::FieldFunction>> ff_list;
ff_list.push_back(std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
));
const size_t num_m0_dofs = sdm.GetNumLocalDOFs(m0_uk_man);
std::vector<double> m0_phi(num_m0_dofs, 0.0);
sdm.CopyVectorWithUnknownScope(phi_tally,
m0_phi,
phi_uk_man,
0,
m0_uk_man,
0);
ff_list[0]->UpdateFieldVector(m0_phi);
chi_physics::FieldFunction::FFList const_ff_list;
for (const auto& ff_ptr : ff_list)
const_ff_list.push_back(ff_ptr);
chi_physics::FieldFunction::ExportMultipleToVTK(fname,
const_ff_list);
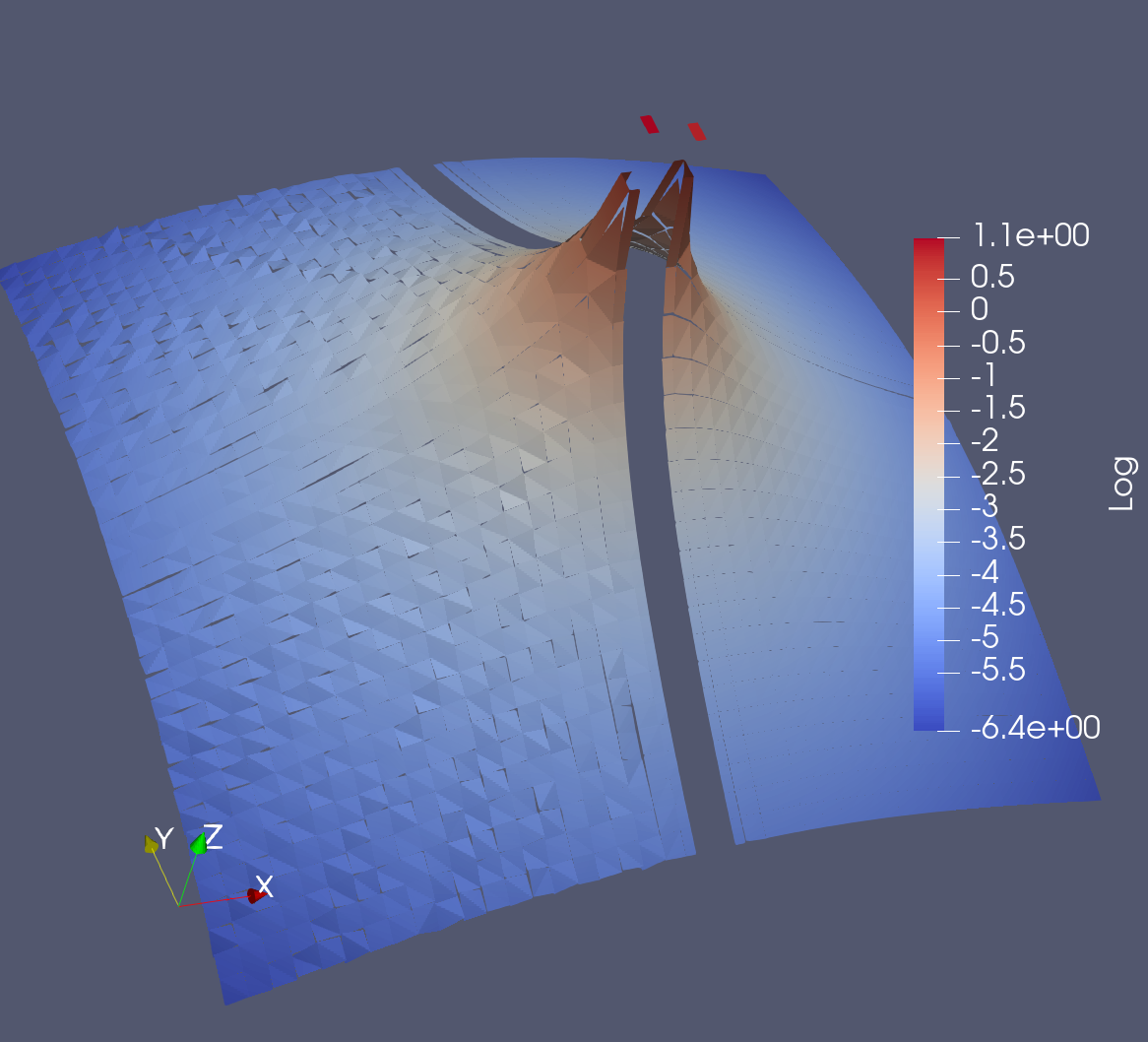
The visualization below shows a logarithmic scale warp of the flux values for both the uncollided algorithm and a LBS simulation using a product quadrature with 96 azimuthal angles and 48 polar angles per octant (18,432 directions total).
The left of the figure is the uncollided algorithm and the right is LBS. Notice the stochastic "noise" from the uncollided algorithm.
The complete program
#include "chi_lua.h"
#include "math/SpatialDiscretization/FiniteElement/PiecewiseLinear/pwl.h"
#include "physics/FieldFunction/fieldfunction2.h"
namespace chi_unit_sim_tests
{
int chiSimTest93_RayTracing(lua_State* Lstate)
{
const std::string fname = "chiSimTest93_RayTracing";
chi::log.Log() << "chiSimTest93_RayTracing";
const auto& grid = *grid_ptr;
chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
const size_t num_groups = 1;
const size_t scattering_order = 1;
const auto& L = scattering_order;
const size_t num_moments =
(dimension == 1)? L + 1 :
(dimension == 2)? (L+1)*(L+2)/2 :
(dimension == 3)? (L+1)*(L+1) : 0;
const double sigma_t = 0.27;
std::vector<std::pair<int,int>> m_to_ell_em_map;
if (dimension == 1)
for (int ell=0; ell<=scattering_order; ell++)
m_to_ell_em_map.emplace_back(ell,0);
else if (dimension == 2)
for (int ell=0; ell<=scattering_order; ell++)
for (int m=-ell; m<=ell; m+=2)
m_to_ell_em_map.emplace_back(ell,m);
else if (dimension == 3)
for (int ell=0; ell<=scattering_order; ell++)
for (int m=-ell; m<=ell; m++)
m_to_ell_em_map.emplace_back(ell,m);
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_PWLD::New(grid_ptr);
const auto& sdm = *sdm_ptr;
for (size_t m=0; m<num_moments; ++m)
const size_t num_fem_local_dofs = sdm.GetNumLocalDOFs(phi_uk_man);
const size_t num_fem_globl_dofs = sdm.GetNumGlobalDOFs(phi_uk_man);
chi::log.Log() << "Num local FEM DOFs: " << num_fem_local_dofs;
chi::log.Log() << "Num globl FEM DOFs: " << num_fem_globl_dofs;
std::vector<double> phi_tally(num_fem_local_dofs, 0.0);
struct Particle
{
Vec3 position = {0.0,0.0,0.0};
Vec3 direction = {0.0,0.0,0.0};
int energy_group = 0;
double weight = 1.0;
uint64_t cell_id = 0;
bool alive = true;
};
const Vec3 source_pos = {0.0,0.0,0.0};
for (auto& cell : grid.local_cells)
if (grid.CheckPointInsideCell(cell, source_pos))
{
source_cell_ptr = &cell;
break;
}
if (source_cell_ptr == nullptr)
throw std::logic_error(fname + ": Source cell not found.");
const uint64_t source_cell_id = source_cell_ptr->global_id;
auto SampleRandomDirection = [&rng]()
{
double costheta = 2.0*rng.
Rand() - 1.0;
double theta = acos(costheta);
double varphi = rng.
Rand()*2.0*M_PI;
sin(theta) * sin(varphi),
cos(theta)};
};
auto ContributePWLDTally = [&sdm,&grid,&phi_tally,&phi_uk_man,&sigma_t,
&num_moments,&m_to_ell_em_map](
const Vec3& positionA,
const Vec3& positionB,
const Vec3& omega,
const int g,
double weight)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const size_t num_nodes = cell_mapping.NumNodes();
const double phi = phi_theta.first;
const double theta = phi_theta.second;
std::vector<double> segment_lengths;
cell,
positionA,
positionB,
omega,
segment_lengths);
std::vector<double> shape_values_k;
std::vector<double> shape_values_kp1;
cell_mapping.ShapeValues(positionA,
shape_values_k);
double d_run_sum = 0.0;
for (const auto& segment_length_k : segment_lengths)
{
d_run_sum += segment_length_k;
const double& d = d_run_sum;
cell_mapping.ShapeValues(positionA+omega*d, shape_values_kp1);
const auto& b_ik = shape_values_k;
const auto& b_ikp1 = shape_values_kp1;
const double& ell_k = segment_length_k;
for (size_t i=0; i<num_nodes; ++i)
{
const double C0 = b_ik[i] * ell_k;
const double C1 = b_ikp1[i] - b_ik[i];
for (size_t m=0; m < num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
const auto& ell_em = m_to_ell_em_map.at(m);
const int ell = ell_em.first;
const int em = ell_em.second;
double w_exp = (C0 / sigma_t) * (1.0 - exp(-sigma_t * ell_k)) +
(C1 / (sigma_t * sigma_t)) *
(1.0 - (1 + sigma_t * ell_k) * exp(-sigma_t * ell_k));
w_exp *= weight / (ell_k * ell_k);
double w_avg = w_harmonic * w_exp;
phi_tally[dof_map] += ell_k * w_avg ;
}
}
shape_values_k = shape_values_kp1;
weight *= exp(-sigma_t * segment_length_k);
}
};
{
const auto& v0 = grid.vertices[cell.vertex_ids[0]];
double xmin = v0.x, xmax = v0.x;
double ymin = v0.y, ymax = v0.y;
double zmin = v0.z, zmax = v0.z;
for (uint64_t vid : cell.vertex_ids)
{
const auto& v = grid.vertices[vid];
xmin = std::min(xmin, v.x); xmax = std::max(xmax, v.x);
ymin = std::min(ymin, v.y); ymax = std::max(ymax, v.y);
zmin = std::min(zmin, v.z); zmax = std::max(zmax, v.z);
}
};
std::vector<double> cell_sizes(grid.local_cells.size(), 0.0);
for (const auto& cell : grid.local_cells)
cell_sizes[cell.local_id] = GetCellApproximateSize(cell);
const size_t num_particles = 1'000'000;
for (size_t n=0; n<num_particles; ++n)
{
if (n % size_t(num_particles/10.0) == 0)
std::cout << "#particles = " << n << "\n";
const auto omega = SampleRandomDirection();
Particle particle{source_pos,
omega,
0,
1.0,
source_cell_id,
true};
while (particle.alive)
{
const auto& cell = grid.cells[particle.cell_id];
auto destination_info = ray_tracer.TraceRay(cell,
particle.position,
particle.direction);
const Vec3& end_of_track_position = destination_info.pos_f;
ContributePWLDTally(cell,
particle.position,
end_of_track_position,
particle.direction,
particle.energy_group,
particle.weight);
if (not destination_info.particle_lost)
{
const auto& f = destination_info.destination_face_index;
const auto& current_cell_face = cell.faces[f];
if (current_cell_face.has_neighbor)
particle.cell_id = current_cell_face.neighbor_id;
else
particle.alive = false;
}
else
{
std::cout << "particle" << n << " lost "
<< particle.position.PrintStr() << " "
<< particle.direction.PrintStr() << " "
<< "\n";
break;
}
const auto& pA = particle.position;
const auto& pB = end_of_track_position;
particle.weight *= exp(-sigma_t*(pB-pA).Norm());
particle.position = end_of_track_position;
}
}
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& qp_data = cell_mapping.MakeVolumeQuadraturePointData();
const size_t num_nodes = cell_mapping.NumNodes();
for (auto qp : qp_data.QuadraturePointIndices())
for (size_t i=0; i<num_nodes; ++i)
for (size_t j=0; j<num_nodes; ++j)
M[i][j] += qp_data.ShapeValue(i,qp) * qp_data.ShapeValue(j, qp) *
qp_data.JxW(qp);
for (size_t m=0; m<num_moments; ++m)
for (size_t g=0; g<num_groups; ++g)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
T[i] = phi_tally[imap] / num_particles;
}
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t imap = sdm.MapDOFLocal(cell, i, phi_uk_man, m, g);
phi_tally[imap] = phi_uc[i];
}
}
}
std::vector<std::shared_ptr<chi_physics::FieldFunction>> ff_list;
ff_list.push_back(std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
));
const size_t num_m0_dofs = sdm.GetNumLocalDOFs(m0_uk_man);
std::vector<double> m0_phi(num_m0_dofs, 0.0);
sdm.CopyVectorWithUnknownScope(phi_tally,
m0_phi,
phi_uk_man,
0,
m0_uk_man,
0);
ff_list[0]->UpdateFieldVector(m0_phi);
chi_physics::FieldFunction::FFList const_ff_list;
for (const auto& ff_ptr : ff_list)
const_ff_list.push_back(ff_ptr);
chi_physics::FieldFunction::ExportMultipleToVTK(fname,
const_ff_list);
return 0;
}
}


![]() amount of tracks traced inside a volume,
amount of tracks traced inside a volume, ![]() , originating from a sample of
, originating from a sample of ![]() number of particles/rays, the scalar flux,
number of particles/rays, the scalar flux, ![]() , can be estimated with
, can be estimated with ![]()
![]() is the
is the ![]() -th track length. This simply means that the scalar flux is the "average track length per unit volume".
-th track length. This simply means that the scalar flux is the "average track length per unit volume".![]() , enabling a multitude of features.
, enabling a multitude of features. ![]()
![]() -th track we simply set the weight to the spherical harmonic evaluated with the direction,
-th track we simply set the weight to the spherical harmonic evaluated with the direction, ![]() , of the track,
, of the track, ![]()
![]() . Therefore we seek
. Therefore we seek ![]() such that
such that ![]()
![]() we need to solve the cell-by-cell system defined by
we need to solve the cell-by-cell system defined by ![]()
![]() are simply the entries of the mass matrix,
are simply the entries of the mass matrix, ![]() , and we still need to find the rhs-entries
, and we still need to find the rhs-entries ![]() . This is where we will use the track length based estimators by weighting with the shape functions b_i.
. This is where we will use the track length based estimators by weighting with the shape functions b_i.![]()
![]()
![]() to
to ![]() .
. 
![]() needs to be split into tracks
needs to be split into tracks ![]() ,
, ![]() and
and ![]() as per the figure. Therefore the integral becomes
as per the figure. Therefore the integral becomes![]()
![]() can be quite expensive so in this particular case it would be better to evaluate the shape function at the half-way point of each segment, after which the integral becomes
can be quite expensive so in this particular case it would be better to evaluate the shape function at the half-way point of each segment, after which the integral becomes ![]()
![]() , along the path of a ray with direction
, along the path of a ray with direction ![]() is expressed as
is expressed as ![]()
![]() is the distance traveled and
is the distance traveled and ![]() is the total cross section. From this model we can compute the attenuation across a cell, with constant
is the total cross section. From this model we can compute the attenuation across a cell, with constant ![]() , as
, as ![]()
![]() is the value of
is the value of ![]() when it entered the cell.
when it entered the cell.![]() , which acts as the proxy for
, which acts as the proxy for ![]() (i.e.,
(i.e., ![]() ). From this we can determine the nodal uncollided flux,
). From this we can determine the nodal uncollided flux, ![]() , in a similar fashion as we would determine the regular flux, i.e.,
, in a similar fashion as we would determine the regular flux, i.e., ![]()
![]() , for which we have
, for which we have ![]()
![]()
![]() is a function of position, specifically
is a function of position, specifically ![]()
![]() .
.![]()
![]() is the track length of the
is the track length of the ![]() -th segment and
-th segment and ![]() is the average weight of this segment. The weight is computed with
is the average weight of this segment. The weight is computed with ![]()
![]() and
and ![]() are the beginning and ending positions of segment
are the beginning and ending positions of segment ![]() respectively.
respectively.![]() , we can compute
, we can compute ![]() at any point along track
at any point along track ![]() including at the start of any segment. Therefore we define
including at the start of any segment. Therefore we define ![]() which allows us to express
which allows us to express ![]() as
as ![]()
![]()
![]() and
and ![]() are the basis function values at the beginning and end of the segment, respectively. These two expressions allow us to evaluate the segment average weight as
are the basis function values at the beginning and end of the segment, respectively. These two expressions allow us to evaluate the segment average weight as ![]()
![]() we can simplify this expression as
we can simplify this expression as![\begin{align*} w_{tk}^{i,avg} &= \frac{1}{\ell_{tk}} \int_{0}^{\ell_{tk}} w_k^p e^{-\sigma_t s' } \biggr[ b_{i,k} \frac{\ell_{tk}-s'}{\ell_{tk}} + b_{i,k+1} \frac{s'}{\ell_{tk}} \biggr] ds' \\ &= \frac{1}{\ell_{tk}^2} \int_{0}^{\ell_{tk}} w_k^p e^{-\sigma_t s' } \biggr[ b_{i,k} \ell_{tk} + (b_{i,k+1} - b_{i,k} ) s' \biggr] ds' \end{align*}](../../form_296.png)
![]()
![]()
![]()
![]()
![]() whilst the polar angle is determined by sampling the cosine of the polar angle uniformly, i.e.,
whilst the polar angle is determined by sampling the cosine of the polar angle uniformly, i.e., ![]() .
.![]() pair. The latter will be used for the harmonic weighting.
pair. The latter will be used for the harmonic weighting.![]() since this will be at position A.
since this will be at position A. ![]() and rename both sets of shape function values and the segment length for convenience.
and rename both sets of shape function values and the segment length for convenience.![]()
![]() to
to ![]() , preventing us from having to compute the values at
, preventing us from having to compute the values at ![]() again (which can be expensive). We also apply the exponential attenuation to the particle weight over the segment.
again (which can be expensive). We also apply the exponential attenuation to the particle weight over the segment. ![]() such that
such that ![]()
![]()
![]() and
and ![]() . Since the mass matrix is such a small matrix we just directly invert it to be used for all groups and moments.
. Since the mass matrix is such a small matrix we just directly invert it to be used for all groups and moments.![]() to the normalized tally values. Thereafter we multiply
to the normalized tally values. Thereafter we multiply ![]() from the left with
from the left with ![]() to get
to get ![]() . Finally we reuse the tally data and set the nodal values of the tally to the uncollided projected flux.
. Finally we reuse the tally data and set the nodal values of the tally to the uncollided projected flux.