Table of contents
1 The multigroup Discrete Ordinates Equations
In this tutorial we look at the multigroup discrete ordinates (DO) equations, otherwise known as the 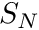 equations. For a complete tutorial, on how these equations are derived, please consult this whitepaper.
equations. For a complete tutorial, on how these equations are derived, please consult this whitepaper.
We start with the equations themselves
![\[ \biggr(\boldsymbol{\Omega}_n \boldsymbol{\cdot} \boldsymbol{\nabla} +\sigma_{tg} (\mathbf{x})\biggr) \psi_{gn} (\mathbf{x})= \sum_{m=0}^{N_m - 1} \frac{2\ell+1}{4\pi}Y_{\ell m^*}(\boldsymbol{\Omega}_n) \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g} (\mathbf{x}) \ \phi_{mg'}(\mathbf{x}) \biggr] + q_{g,n} (\mathbf{x}) \quad \quad \quad \mathbf{x}\in\mathcal{D} \]](../../form_194.png)
![\[ \psi_{gn}(\mathbf{x}) =0 \quad \quad \quad \mathbf{x}\in\partial\mathcal{D} \]](../../form_195.png)
where the variables have the following meaning
The "angular quadrature" mentioned here contains considerable history. When the DO-method was still in it's infancy, most simulations were still one dimensional. In such cases the angular flux has no azimuthal dependence and the angular integrals reduce to Gauss-Legendre quadratures. Because the DO-method generally avoids the placement of a quadrature point on the 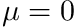 plane, it was generally preferred to use quadratures with even-amounts of quadrature points. Because of this, people in the transport community typically referred to the DO-method as the
plane, it was generally preferred to use quadratures with even-amounts of quadrature points. Because of this, people in the transport community typically referred to the DO-method as the 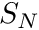 method with
method with 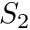 being the first even quadrature used, followed by
being the first even quadrature used, followed by 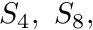 etc.
etc.
In two and three dimensions, where one generally have dependence on both the azimuthal and polar directions (although 2D is symmetric in the polar angle), the nomenclature could be extended with the use of the "so-called" triangular quadratures. These type of quadratures placed ever decreasing amount of polar angles starting from the equator of the unit sphere towards the poles. Incidentally, if the number of polar angles per octant is 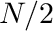 then the azimuthal "level" closest to the equator will start with
then the azimuthal "level" closest to the equator will start with 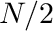 number of azimuthal angles. For example, an
number of azimuthal angles. For example, an 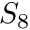 angular quadrature in 3D has 4 polar levels per octant, therefore the azimuthal angles would start at 4, then 3, then 2, then 1 at the polar-lelel closest to the pole.
angular quadrature in 3D has 4 polar levels per octant, therefore the azimuthal angles would start at 4, then 3, then 2, then 1 at the polar-lelel closest to the pole.
The use of the triangular quadratures are considered to be quite antiquated. Some of the reasons for this includes the following:
- When more resolution in the azimuthal domain is required then a higher
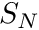 order will unfortunately be accompanied by more polar angles.
order will unfortunately be accompanied by more polar angles.
- In 2D, the polar dependence can accurately be captured with just a few polar angles, however, the azimuthal dependence may still be unresolved. Product quadratures are then best suited to place more azimuthal directions in the quadrature.
- Generally, 3D simulations (e.g. reactor simulations) depend more strongly on the azimuthal directions than on the polar directions.
In ChiTech we have a wide array of angular quadratures to choose from.
For this tutorial we will be looking at the following test problem
The domain spans from -1 to +1 in both dimensions. We define a source in the sub-domain -0.5 to +0.5 in both dimensions. The source strength is 1 in group 0 only.
2 The Diamond Difference Spatial Discretization
The Diamond Difference (DD) spatial discretization is a precursor to the Weighted Diamond Difference (WDD) spatial discretization. Fundamentally, it is a Finite Volume based spatial discretization.
2.1 The right hand side
Since we are dealing with a FV discretization the values of cross sections, fluxes and sources are cell constant. Therefore, the RHS of the multigroup DO equations becomes
![\[ q_c^{rhs} = \sum_{m=0}^{N_m - 1} \frac{2\ell+1}{4\pi}Y_{\ell m^*}(\boldsymbol{\Omega}_n) \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g,c} \ \phi_{mg',c} \biggr] + \frac{1}{4\pi} q_{g,c}. \]](../../form_213.png)
This representation is, however, not very practical and instead we choose to write it as
![\[ q_{c,g}^{rhs} = \sum_{m=0}^{N_m-1} M_{mn} q_{c,g}^{moms,m} \]](../../form_214.png)
where 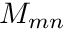 is called the Moment-To-Discrete operator (on a nodal level) and defined as
is called the Moment-To-Discrete operator (on a nodal level) and defined as
![\[ M_{mn} = \frac{2\ell+1}{4\pi}Y_{\ell m^*}(\boldsymbol{\Omega}_n) \]](../../form_216.png)
noting that 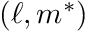 is mapped from
is mapped from 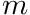 . This operator can be precomputed once the angular quadrature is known. The other quantity introduced here,
. This operator can be precomputed once the angular quadrature is known. The other quantity introduced here, 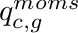 , is called the source moments for cell
, is called the source moments for cell 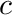 group
group 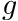 and is defined by
and is defined by
![\[ q_{c,g}^{moms,m} = \begin{cases} \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g,c} \ \phi_{mg',c} \biggr] + q_{c,g} \quad \quad &m=0,\\ \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g,c} \ \phi_{mg',c} \biggr] \quad \quad &m\ne 0 \end{cases} \]](../../form_219.png)
In the iterative schemes, that will be introduced later, we compute and store a vector of source moments for each iteration.
2.2 The left hand side
With the simplified definition of the RHS we now need to address the discretization of the divergence term in the DO equations.
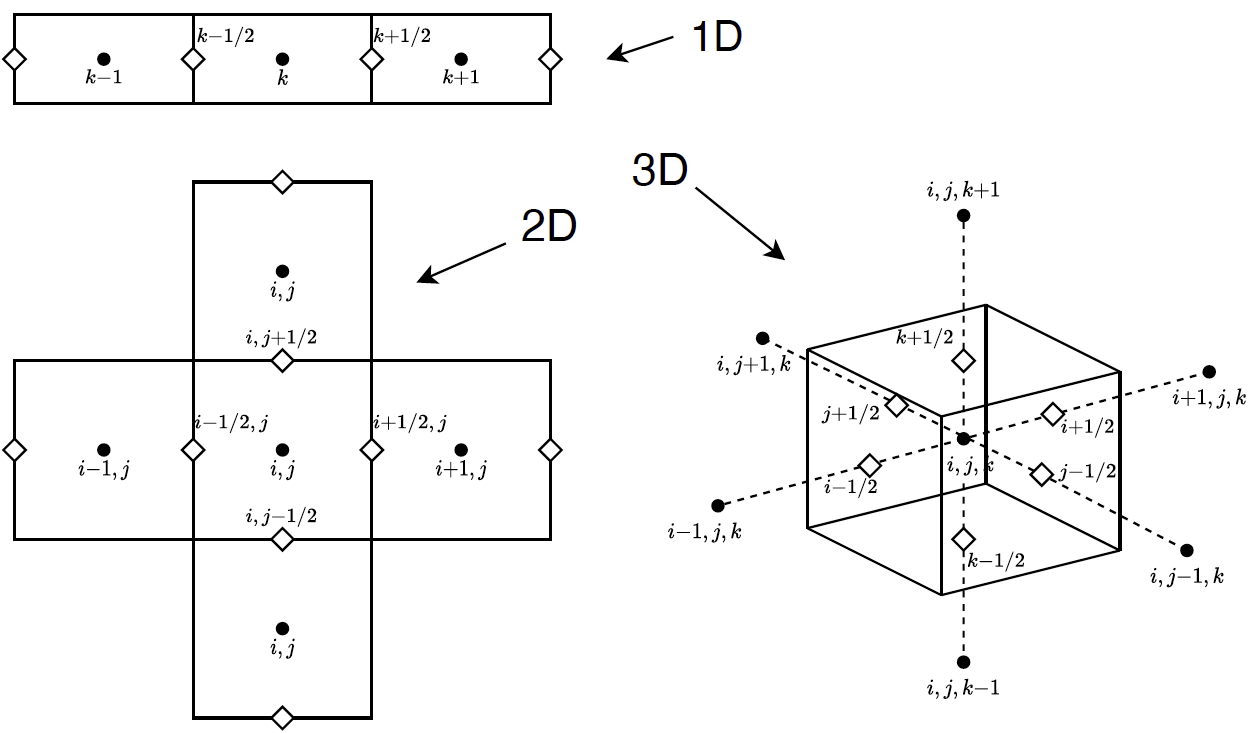
The DD approximation uses convention as shown in the figure below
With this convention we've introduced nodes on the interstitial faces between cells. Suppressing, for the moment, direction and group indices, we can express the divergence term as
![\[ \boldsymbol{\Omega} \boldsymbol{\cdot} \boldsymbol{\nabla} \psi = \Omega_x \frac{\partial \psi}{\partial x} + \Omega_y \frac{\partial \psi}{\partial y} + \Omega_z \frac{\partial \psi}{\partial z}. \]](../../form_220.png)
We then introduce the approximation, e.g., in the x-dimension
![\[ \Omega_x \frac{\partial \psi}{\partial x} = \frac{\Omega_x}{\Delta x} (\psi_{i+\frac{1}{2}} - \psi_{i-\frac{1}{2}}) \]](../../form_221.png)
which, if done for all the dimensions, introduces up to 6 new variables into the equation. Fortunately, since we can apply upwinding, we can eliminate half of these with the closure relation
![\[ \psi_i = \frac{1}{2}(\psi_{i+\frac{1}{2}} + \psi_{i-\frac{1}{2}}), \]](../../form_222.png)
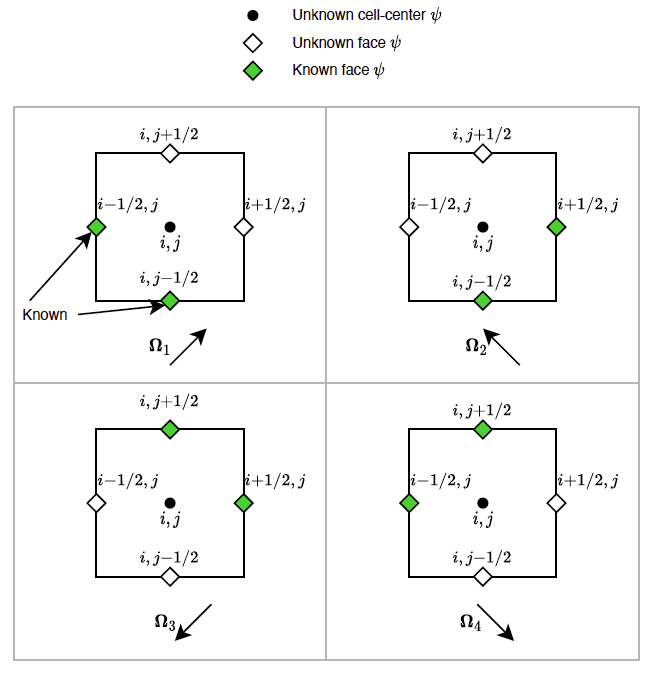
obviously extended to all dimensions. To comprehend this upwinding, consider the schematic below, showing the upwinding for different configurations of 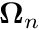 .
.
With upwinding defined we can re-express the upwinded angular flux as 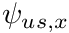 being either
being either 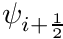 or
or 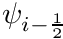 depending on the sign of
depending on the sign of 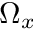 . The
. The 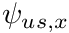 of the current cell would then be the downstream flux,
of the current cell would then be the downstream flux, 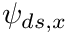 of the adjacent cell at the interstitial face. With some manipulation we arrive at the following equations to solve the current cell's
of the adjacent cell at the interstitial face. With some manipulation we arrive at the following equations to solve the current cell's 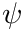 :
:
as well as the following equations to obtain its downstream angular flux:
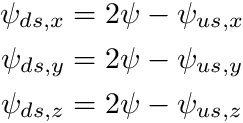
The solution procedure, per cell, is therefore to first grab 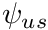 as either the upstream cell's
as either the upstream cell's 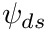 or from the upstream boundary condition. Then to solve for the cell
or from the upstream boundary condition. Then to solve for the cell 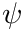 . Then to compute
. Then to compute 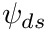 .
.
The obvious difficulty now is to loop through the cells in such a way that the upstream relationships, with respect to a given 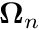 , is maintained. This process is known as sweeping. And for orthogonal grids it looks like shown in the figure below
, is maintained. This process is known as sweeping. And for orthogonal grids it looks like shown in the figure below
3 Getting the grid with additional preoperties
We get the grid in the same fashion as we did in all the previous tutorial, however, this time need to get some additional information since we will use it during the sweep.
We define the following code once we obtained a reference to the grid
const auto ijk_info = grid.GetIJKInfo();
const auto& ijk_mapping = grid.MakeIJKToGlobalIDMapping();
const auto cell_ortho_sizes = grid.MakeCellOrthoSizes();
const auto Nx = static_cast<int64_t>(ijk_info[0]);
const auto Ny = static_cast<int64_t>(ijk_info[1]);
const auto Nz = static_cast<int64_t>(ijk_info[2]);
int dimension = 0;
if (grid.Attributes() & Dim1) dimension = 1;
if (grid.Attributes() & Dim2) dimension = 2;
if (grid.Attributes() & Dim3) dimension = 3;
The structure ijk_info holds an array holding the number of cells in x,y and z. The structure ijk_mapping holds a mapping, given a cell's ijk index, to the linear global mapping. The structure cell_ortho_size contains a std::vector of cell 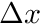 ,
, 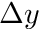 and
and 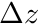 . We finally also assign the dimensionality of the mesh to an integer
. We finally also assign the dimensionality of the mesh to an integer dimension.
4 Creating an angular quadrature
The base class for angular quadratures is chi_math::AngularQuadrature.
std::shared_ptr<chi_math::AngularQuadrature> quadrature;
if (dimension == 1)
quadrature = std::make_shared<chi_math::AngularQuadratureProdGL>(8);
else if (dimension == 2)
{
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
quadrature->OptimizeForPolarSymmetry(4.0*M_PI);
}
else if (dimension == 3)
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
else
throw std::logic_error(fname + "Error with the dimensionality "
"of the mesh.");
chi::log.Log() << "Quadrature created." << std::endl;
Depending on the dimensionality of the grid we instate a different quadrature set. For example, in one dimension we instantiate the Gauss-Legendre quadrature encapsulated in a product quadrature, chi_math::AngularQuadratureProdGL.
quadrature = std::make_shared<chi_math::AngularQuadratureProdGL>(8);
where the parameter is the number of polar angles per hemisphere.
In two and three dimensions we instantiate the Gauss-Legendre-Chebyshev quadrature encapsulated in a product quadrature, chi_math::AngularQuadratureProdGLC.
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
A GLC quadrature is essentially an evenly spaced quadrature in the azimuthal space and a regular Legendre spacing in the polar space. The parameters are the number of azimuthal angles per octant and the number of polar angles per octant.
For the 2D case, which has polar symmetry, we can modify the quadrature to only contain the directions in the upper hemisphere. We do this as
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
quadrature->OptimizeForPolarSymmetry(4.0*M_PI);
The argument for OptimizeForPolarSymmetry is the normalization factor to use when normalizing the quadrature.
Since we now have the angular quadrature we can compute the Moment-To-Discrete and Discrete-To-Moment operator.
const size_t scat_order = 1;
const size_t num_groups = 20;
quadrature->BuildMomentToDiscreteOperator(scat_order,dimension);
quadrature->BuildDiscreteToMomentOperator(scat_order,dimension);
const auto& m2d = quadrature->GetMomentToDiscreteOperator();
const auto& d2m = quadrature->GetDiscreteToMomentOperator();
const auto& m_ell_em_map = quadrature->GetMomentToHarmonicsIndexMap();
const size_t num_moments = m_ell_em_map.size();
const size_t num_dirs = quadrature->omegas.size();
chi::log.Log() << "End Set/Get params." << std::endl;
chi::log.Log() << "Num Moments: " << num_moments << std::endl;
Notice we also obtained the mapping from 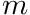 to
to 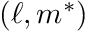 in the structure
in the structure m_ell_em_map which contains a list of chi_math::AngularQuadrature::HarmonicIndices.
5 Auxialiary items
We define the auxiliary items as follows
std::vector<Unknown> phi_uks(num_moments, Unknown(VecN, num_groups));
std::vector<Unknown> psi_uks(num_dirs, Unknown(VecN, num_groups));
const size_t num_local_phi_dofs = sdm.GetNumLocalDOFs(phi_uk_man);
const size_t num_local_psi_dofs = sdm.GetNumLocalDOFs(psi_uk_man);
chi::log.Log() << "End ukmanagers." << std::endl;
chi_physics::TransportCrossSections xs;
xs.MakeFromCHIxsFile("tests/xs_graphite_pure.cxs");
std::vector<double> phi_old(num_local_phi_dofs,0.0);
std::vector<double> psi(num_local_psi_dofs, 0.0);
auto source_moments = phi_old;
auto phi_new = phi_old;
auto q_source = phi_old;
chi::log.Log() << "End vectors." << std::endl;
for (const auto& cell : grid.local_cells)
{
const auto& cc = cell.centroid;
const auto& cell_mapping = sdm.GetCellMapping(cell);
const size_t num_nodes = cell_mapping.NumNodes();
if (cc.x < 0.5 and cc.y < 0.5 and cc.z < 0.5 and
cc.x >-0.5 and cc.y >-0.5 and cc.z >-0.5)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,i,phi_uk_man,0,0);
q_source[dof_map] = 1.0;
}
}
}
First is the unknown managers for 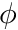 and
and 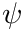 . Then transport cross sections via the class
. Then transport cross sections via the class chi_physics::TransportCrossSections.
We then define the unknown vectors.
std::vector<double> phi_old(num_local_phi_dofs,0.0);
std::vector<double> psi(num_local_psi_dofs, 0.0);
auto source_moments = phi_old;
auto phi_new = phi_old;
auto q_source = phi_old;
chi::log.Log() << "End vectors." << std::endl;
Finally, we hardcode the source distribution
for (const auto& cell : grid.local_cells)
{
const auto& cc = cell.centroid;
const auto& cell_mapping = sdm.GetCellMapping(cell);
const size_t num_nodes = cell_mapping.NumNodes();
if (cc.x < 0.5 and cc.y < 0.5 and cc.z < 0.5 and
cc.x >-0.5 and cc.y >-0.5 and cc.z >-0.5)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,i,phi_uk_man,0,0);
q_source[dof_map] = 1.0;
}
}
}
6 Defining a cell-by-cell sweep chunk
IJKArrayDbl psi_ds_x(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
IJKArrayDbl psi_ds_y(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
IJKArrayDbl psi_ds_z(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
auto SweepChunk = [&ijk_info, &ijk_mapping, &cell_ortho_sizes,
&grid, &sdm,
&num_moments,
&phi_uk_man, &psi_uk_man,
&m2d,&d2m,
&phi_new, &source_moments, &psi,
&psi_ds_x, &psi_ds_y, &psi_ds_z]
(const std::array<int64_t,3>& ijk,
const Vec3& omega,
const size_t d,
const chi_physics::TransportCrossSections& cell_xs)
{
const auto cell_global_id = ijk_mapping.MapNDtoLin(ijk[1],ijk[0],ijk[2]);
const auto& cell = grid.cells[cell_global_id];
const auto cell_local_id = cell.local_id;
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& cell_ortho_size = cell_ortho_sizes[cell_local_id];
const double dx = cell_ortho_size.x;
const double dy = cell_ortho_size.y;
const double dz = cell_ortho_size.z;
const std::vector<double> zero_vector(num_groups,0.0);
const double* psi_us_x = zero_vector.data();
const double* psi_us_y = zero_vector.data();
const double* psi_us_z = zero_vector.data();
const auto i = ijk[0]; const auto Nx = ijk_info[0];
const auto j = ijk[1]; const auto Ny = ijk_info[1];
const auto k = ijk[2]; const auto Nz = ijk_info[2];
if (omega.x > 0.0 and i > 0 ) psi_us_x = &psi_ds_x(i-1,j ,k ,0);
if (omega.x < 0.0 and i < (Nx-1)) psi_us_x = &psi_ds_x(i+1,j ,k ,0);
if (omega.y > 0.0 and j > 0 ) psi_us_y = &psi_ds_y(i ,j-1,k ,0);
if (omega.y < 0.0 and j < (Ny-1)) psi_us_y = &psi_ds_y(i ,j+1,k ,0);
if (omega.z > 0.0 and k > 0 ) psi_us_z = &psi_ds_z(i ,j ,k-1,0);
if (omega.z < 0.0 and k < (Nz-1)) psi_us_z = &psi_ds_z(i ,j ,k+1,0);
for (size_t g=0; g<num_groups; ++g)
{
double rhs = 0.0;
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
rhs += source_moments[dof_map]*m2d[m][d];
}
if (Nx > 1) rhs += 2.0*std::fabs(omega.x)*psi_us_x[g]/dx;
if (Ny > 1) rhs += 2.0*std::fabs(omega.y)*psi_us_y[g]/dy;
if (Nz > 1) rhs += 2.0*std::fabs(omega.z)*psi_us_z[g]/dz;
double lhs = cell_xs.sigma_t[g];
if (Nx > 1) lhs += 2.0*std::fabs(omega.x)/dx;
if (Ny > 1) lhs += 2.0*std::fabs(omega.y)/dy;
if (Nz > 1) lhs += 2.0*std::fabs(omega.z)/dz;
double psi_ijk = rhs/lhs;
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
phi_new[dof_map] += d2m[m][d]*psi_ijk;
}
const int64_t psi_map = sdm.MapDOFLocal(cell,0,psi_uk_man,d,g);
psi[psi_map] = psi_ijk;
psi_ds_x(i,j,k,g) = 2.0*psi_ijk - psi_us_x[g];
psi_ds_y(i,j,k,g) = 2.0*psi_ijk - psi_us_y[g];
psi_ds_z(i,j,k,g) = 2.0*psi_ijk - psi_us_z[g];
}
};
The first portion of the chunk is obtaining all the relevant cell information
const auto cell_global_id = ijk_mapping.MapNDtoLin(ijk[1],ijk[0],ijk[2]);
const auto& cell = grid.cells[cell_global_id];
const auto cell_local_id = cell.local_id;
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& cell_ortho_size = cell_ortho_sizes[cell_local_id];
const double dx = cell_ortho_size.x;
const double dy = cell_ortho_size.y;
const double dz = cell_ortho_size.z;
const auto i = ijk[0]; const auto Nx = ijk_info[0];
const auto j = ijk[1]; const auto Ny = ijk_info[1];
const auto k = ijk[2]; const auto Nz = ijk_info[2];
Thereafter we determine the upstream fluxes from the general downstream 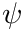 structures. These data structures are multidimensional arrays
structures. These data structures are multidimensional arrays chi_data_types::NDArray which are used to store each cell's downstream components. These arrays are indexed with ijk indices making them easy to use in our orthogonal mesh setting.
const std::vector<double> zero_vector(num_groups,0.0);
const double* psi_us_x = zero_vector.data();
const double* psi_us_y = zero_vector.data();
const double* psi_us_z = zero_vector.data();
if (omega.x > 0.0 and i > 0 ) psi_us_x = &psi_ds_x(i-1,j ,k ,0);
if (omega.x < 0.0 and i < (Nx-1)) psi_us_x = &psi_ds_x(i+1,j ,k ,0);
if (omega.y > 0.0 and j > 0 ) psi_us_y = &psi_ds_y(i ,j-1,k ,0);
if (omega.y < 0.0 and j < (Ny-1)) psi_us_y = &psi_ds_y(i ,j+1,k ,0);
if (omega.z > 0.0 and k > 0 ) psi_us_z = &psi_ds_z(i ,j ,k-1,0);
if (omega.z < 0.0 and k < (Nz-1)) psi_us_z = &psi_ds_z(i ,j ,k+1,0);
Finally, we loop over each group then construct and solve the relevant equations.
First we develop the angular source from the source moments
![\[ q_{c,g}^{rhs} = \sum_{m=0}^{N_m-1} M_{mn} q_{c,g}^{moms,m} \]](../../form_214.png)
double rhs = 0.0;
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
rhs += source_moments[dof_map]*m2d[m][d];
}
Thereafter we construct and solve the equation for 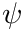 ,
,
for which we have the code
if (Nx > 1) rhs += 2.0*std::fabs(omega.x)*psi_us_x[g]/dx;
if (Ny > 1) rhs += 2.0*std::fabs(omega.y)*psi_us_y[g]/dy;
if (Nz > 1) rhs += 2.0*std::fabs(omega.z)*psi_us_z[g]/dz;
double lhs = cell_xs.sigma_t[g];
if (Nx > 1) lhs += 2.0*std::fabs(omega.x)/dx;
if (Ny > 1) lhs += 2.0*std::fabs(omega.y)/dy;
if (Nz > 1) lhs += 2.0*std::fabs(omega.z)/dz;
double psi_ijk = rhs/lhs;
Once we have psi we can contribute to the flux moments
![\[ \phi_{\ell m^*} =\sum_n w_n Y_{\ell m^*}(\boldsymbol{\Omega}_n) \psi_n \]](../../form_235.png)
which maps to
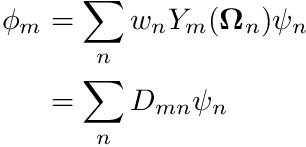
where 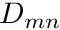 is the Discrete-To-Moment operator. We do the above with the following code
is the Discrete-To-Moment operator. We do the above with the following code
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
phi_new[dof_map] += d2m[m][d]*psi_ijk;
}
Next we store all the angular flux
const int64_t psi_map = sdm.MapDOFLocal(cell,0,psi_uk_man,d,g);
psi[psi_map] = psi_ijk;
psi_ds_x(i,j,k,g) = 2.0*psi_ijk - psi_us_x[g];
psi_ds_y(i,j,k,g) = 2.0*psi_ijk - psi_us_y[g];
psi_ds_z(i,j,k,g) = 2.0*psi_ijk - psi_us_z[g];
7 Defining a sweep over all directions
Next we define a routine that will sweep through cells with the correct upwinding structure for all the directions in the quadrature.
auto Sweep = [&num_dirs,&quadrature,Nx,Ny,Nz,&
SweepChunk,&xs]()
{
for (size_t d=0; d<num_dirs; ++d)
{
const auto &omega = quadrature->omegas[d];
const auto &weight = quadrature->weights[d];
std::vector<int64_t> iorder, jorder, korder;
if (omega.x > 0.0) iorder = chi_math::Range<int64_t>(0, Nx);
else iorder = chi_math::Range<int64_t>(Nx - 1, -1, -1);
if (omega.y > 0.0) jorder = chi_math::Range<int64_t>(0, Ny);
else jorder = chi_math::Range<int64_t>(Ny - 1, -1, -1);
if (omega.z > 0.0) korder = chi_math::Range<int64_t>(0, Nz);
else korder = chi_math::Range<int64_t>(Nz - 1, -1, -1);
for (auto i: iorder)
for (auto j: jorder)
for (auto k: korder)
}
};
chi_mesh::sweep_management::SweepChunk SweepChunk
This kind of code, for the sweep ordering, will only work for orthogonal meshes hence why this tutorial is based on orthogonal meshes.
8 The Classic Richardson iterative scheme
Yup, as easy as this:
chi::log.Log() << "Starting iterations" << std::endl;
for (size_t iter=0; iter<200; ++iter)
{
phi_new.assign(phi_new.size(), 0.0);
source_moments = SetSource(grid,sdm,phi_uk_man,
q_source,phi_old,xs,m_ell_em_map);
Sweep();
const double rel_change = ComputeRelativePWChange(grid,sdm,phi_uk_man,
phi_new, phi_old);
std::stringstream outstr;
outstr << "Iteration " << std::setw(5) << iter << " ";
{
char buffer[100];
sprintf(buffer, "%11.3e\n", rel_change);
outstr << buffer;
}
chi::log.Log() << outstr.str();
phi_old = phi_new;
if (rel_change < 1.0e-6 and iter > 0)
break;
}
Notice here we have defined two routines:
std::vector<double> SetSource(
const std::vector<double>& q_source,
const std::vector<double>& phi_old,
const chi_physics::TransportCrossSections& xs,
const std::vector<YlmIndices>& m_ell_em_map)
{
std::vector<double> source_moments(num_local_phi_dofs, 0.0);
const size_t num_moments = phi_uk_man.unknowns.size();
const size_t num_groups = phi_uk_man.unknowns.front().num_components;
{
const size_t num_nodes = cell_mapping.
NumNodes();
const auto& S = xs.transfer_matrices;
for (size_t i=0; i<num_nodes; ++i)
{
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.
MapDOFLocal(cell,i,phi_uk_man,m,0);
const auto ell = m_ell_em_map[m].ell;
for (size_t g=0; g<num_groups; ++g)
{
source_moments[dof_map + g] = q_source[dof_map + g];
if (ell < S.size())
{
double inscat_g = 0.0;
for (const auto& [row_g, gprime, sigma_sm] : S[ell].Row(g))
inscat_g += sigma_sm * phi_old[dof_map + gprime];
source_moments[dof_map + g] += inscat_g;
}
}
}
}
}
return source_moments;
}
const CellMapping & GetCellMapping(const chi_mesh::Cell &cell) const
size_t GetNumLocalDOFs(const UnknownManager &unknown_manager) const
virtual int64_t MapDOFLocal(const chi_mesh::Cell &cell, unsigned int node, const UnknownManager &unknown_manager, unsigned int unknown_id, unsigned int component) const =0
LocalCellHandler local_cells
and
double ComputeRelativePWChange(
const std::vector<double>& in_phi_new,
const std::vector<double>& in_phi_old
)
{
double pw_change = 0.0;
const size_t num_moments = phi_uk_man.unknowns.size();
const size_t num_groups = phi_uk_man.unknowns.front().num_components;
{
const size_t num_nodes = cell_mapping.
NumNodes();
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t m0_map = sdm.
MapDOFLocal(cell,i,phi_uk_man,0,0);
const double* phi_new_m0 = &in_phi_new[m0_map];
const double* phi_old_m0 = &in_phi_old[m0_map];
for (size_t m=0; m<num_moments; ++m)
{
const int64_t m_map = sdm.
MapDOFLocal(cell,i,phi_uk_man,m,0);
const double* phi_new_m = &in_phi_new[m_map];
const double* phi_old_m = &in_phi_old[m_map];
for (size_t g=0; g<num_groups; ++g)
{
const double abs_phi_new_g_m0 = std::fabs(phi_new_m0[g]);
const double abs_phi_old_g_m0 = std::fabs(phi_old_m0[g]);
const double max_denominator = std::max(abs_phi_new_g_m0,
abs_phi_old_g_m0);
const double delta_phi = std::fabs(phi_new_m[g] - phi_old_m[g]);
if (max_denominator >= std::numeric_limits<double>::min())
pw_change = std::max(delta_phi/max_denominator,pw_change);
else
pw_change = std::max(delta_phi,pw_change);
}
}
}
}
return pw_change;
}
The SetSource routine populates the source_moments vector, while the ComputeRelativePWChange routine computes a modified version of the 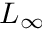 norm by compute the maximum change relative to the scalar moment flux on each node-group pair.
norm by compute the maximum change relative to the scalar moment flux on each node-group pair.
9 Exporting only the scalar flux
We finally want to export the scalar flux to VTK. We have a problem though. The scalar flux is mixed in within the other flux moments. Therefore we need to copy the scalar flux, with the phi_old vector, which has the unknown structure define by phi_uk_man to another vector m0_phi with a different unknown structure. We do this with the following code
std::vector<double> m0_phi(num_m0_dofs, 0.0);
m0_phi,
phi_uk_man,
0,
m0_uk_man,
0);
void CopyVectorWithUnknownScope(const std::vector< double > &from_vector, std::vector< double > &to_vector, const UnknownManager &from_vec_uk_structure, unsigned int from_vec_uk_id, const UnknownManager &to_vec_uk_structure, unsigned int to_vec_uk_id) const
This code should be self explanatory.
Finally we create, update and export the field function like we did with the other tutorials.
auto phi_ff = std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
);
phi_ff->UpdateFieldVector(m0_phi);
phi_ff->ExportToVTK("SimTest_06_WDD");
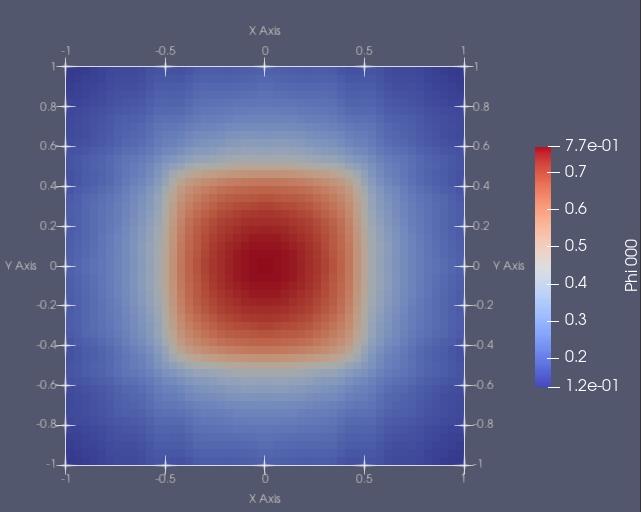
The solution is shown below:
Notice the blocky appearance, a consequence of the finite volume discretization.
The complete program
#include "math/SpatialDiscretization/FiniteVolume/fv.h"
#include "physics/FieldFunction/fieldfunction2.h"
#include "physics/PhysicsMaterial/transportxsections/material_property_transportxsections.h"
int main(
int argc,
char* argv[])
{
chi::Initialize(argc,argv);
chi::RunBatch(argc, argv);
const std::string fname = "Tutorial_06";
if (chi::mpi.process_count != 1)
throw std::logic_error(fname + ": Is serial only.");
const auto& grid = *grid_ptr;
const auto Nx = static_cast<int64_t>(ijk_info[0]);
const auto Ny = static_cast<int64_t>(ijk_info[1]);
const auto Nz = static_cast<int64_t>(ijk_info[2]);
int dimension = 0;
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_FV::New(grid_ptr);
const auto& sdm = *sdm_ptr;
chi::log.Log() << "Num local nodes: " << num_local_nodes;
chi::log.Log() << "Num globl nodes: " << num_globl_nodes;
std::shared_ptr<chi_math::AngularQuadrature> quadrature;
if (dimension == 1)
quadrature = std::make_shared<chi_math::AngularQuadratureProdGL>(8);
else if (dimension == 2)
{
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
quadrature->OptimizeForPolarSymmetry(4.0*M_PI);
}
else if (dimension == 3)
quadrature = std::make_shared<chi_math::AngularQuadratureProdGLC>(8,8);
else
throw std::logic_error(fname + "Error with the dimensionality "
"of the mesh.");
chi::log.Log() << "Quadrature created." << std::endl;
const size_t scat_order = 1;
const size_t num_groups = 20;
quadrature->BuildMomentToDiscreteOperator(scat_order,dimension);
quadrature->BuildDiscreteToMomentOperator(scat_order,dimension);
const auto& m2d = quadrature->GetMomentToDiscreteOperator();
const auto& d2m = quadrature->GetDiscreteToMomentOperator();
const auto& m_ell_em_map = quadrature->GetMomentToHarmonicsIndexMap();
const size_t num_moments = m_ell_em_map.size();
const size_t num_dirs = quadrature->omegas.size();
chi::log.Log() << "End Set/Get params." << std::endl;
chi::log.Log() << "Num Moments: " << num_moments << std::endl;
std::vector<Unknown> phi_uks(num_moments, Unknown(VecN, num_groups));
std::vector<Unknown> psi_uks(num_dirs, Unknown(VecN, num_groups));
chi::log.Log() << "End ukmanagers." << std::endl;
chi_physics::TransportCrossSections xs;
xs.MakeFromCHIxsFile("tests/xs_graphite_pure.cxs");
std::vector<double> phi_old(num_local_phi_dofs,0.0);
std::vector<double> psi(num_local_psi_dofs, 0.0);
auto source_moments = phi_old;
auto phi_new = phi_old;
auto q_source = phi_old;
chi::log.Log() << "End vectors." << std::endl;
{
const auto& cc = cell.centroid;
const size_t num_nodes = cell_mapping.
NumNodes();
if (cc.x < 0.5 and cc.y < 0.5 and cc.z < 0.5 and
cc.x >-0.5 and cc.y >-0.5 and cc.z >-0.5)
{
for (size_t i=0; i<num_nodes; ++i)
{
const int64_t dof_map = sdm.
MapDOFLocal(cell,i,phi_uk_man,0,0);
q_source[dof_map] = 1.0;
}
}
}
IJKArrayDbl psi_ds_x(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
IJKArrayDbl psi_ds_y(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
IJKArrayDbl psi_ds_z(std::array<int64_t,4>{Nx,Ny,Nz,num_groups});
auto SweepChunk = [&ijk_info, &ijk_mapping, &cell_ortho_sizes,
&grid, &sdm,
&num_moments,
&phi_uk_man, &psi_uk_man,
&m2d,&d2m,
&phi_new, &source_moments, &psi,
&psi_ds_x, &psi_ds_y, &psi_ds_z]
(const std::array<int64_t,3>& ijk,
const Vec3& omega,
const size_t d,
const chi_physics::TransportCrossSections& cell_xs)
{
const auto cell_global_id = ijk_mapping.MapNDtoLin(ijk[1],ijk[0],ijk[2]);
const auto& cell = grid.cells[cell_global_id];
const auto cell_local_id = cell.local_id;
const auto& cell_mapping = sdm.GetCellMapping(cell);
const auto& cell_ortho_size = cell_ortho_sizes[cell_local_id];
const double dx = cell_ortho_size.x;
const double dy = cell_ortho_size.y;
const double dz = cell_ortho_size.z;
const auto i = ijk[0]; const auto Nx = ijk_info[0];
const auto j = ijk[1]; const auto Ny = ijk_info[1];
const auto k = ijk[2]; const auto Nz = ijk_info[2];
const std::vector<double> zero_vector(num_groups,0.0);
const double* psi_us_x = zero_vector.data();
const double* psi_us_y = zero_vector.data();
const double* psi_us_z = zero_vector.data();
if (omega.x > 0.0 and i > 0 ) psi_us_x = &psi_ds_x(i-1,j ,k ,0);
if (omega.x < 0.0 and i < (Nx-1)) psi_us_x = &psi_ds_x(i+1,j ,k ,0);
if (omega.y > 0.0 and j > 0 ) psi_us_y = &psi_ds_y(i ,j-1,k ,0);
if (omega.y < 0.0 and j < (Ny-1)) psi_us_y = &psi_ds_y(i ,j+1,k ,0);
if (omega.z > 0.0 and k > 0 ) psi_us_z = &psi_ds_z(i ,j ,k-1,0);
if (omega.z < 0.0 and k < (Nz-1)) psi_us_z = &psi_ds_z(i ,j ,k+1,0);
for (size_t g=0; g<num_groups; ++g)
{
double rhs = 0.0;
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
rhs += source_moments[dof_map]*m2d[m][d];
}
if (Nx > 1) rhs += 2.0*std::fabs(omega.x)*psi_us_x[g]/dx;
if (Ny > 1) rhs += 2.0*std::fabs(omega.y)*psi_us_y[g]/dy;
if (Nz > 1) rhs += 2.0*std::fabs(omega.z)*psi_us_z[g]/dz;
double lhs = cell_xs.sigma_t[g];
if (Nx > 1) lhs += 2.0*std::fabs(omega.x)/dx;
if (Ny > 1) lhs += 2.0*std::fabs(omega.y)/dy;
if (Nz > 1) lhs += 2.0*std::fabs(omega.z)/dz;
double psi_ijk = rhs/lhs;
for (size_t m=0; m<num_moments; ++m)
{
const int64_t dof_map = sdm.MapDOFLocal(cell,0,phi_uk_man,m,g);
phi_new[dof_map] += d2m[m][d]*psi_ijk;
}
const int64_t psi_map = sdm.MapDOFLocal(cell,0,psi_uk_man,d,g);
psi[psi_map] = psi_ijk;
psi_ds_x(i,j,k,g) = 2.0*psi_ijk - psi_us_x[g];
psi_ds_y(i,j,k,g) = 2.0*psi_ijk - psi_us_y[g];
psi_ds_z(i,j,k,g) = 2.0*psi_ijk - psi_us_z[g];
}
};
auto Sweep = [&num_dirs,&quadrature,Nx,Ny,Nz,&
SweepChunk,&xs]()
{
for (size_t d=0; d<num_dirs; ++d)
{
const auto &omega = quadrature->omegas[d];
const auto &weight = quadrature->weights[d];
std::vector<int64_t> iorder, jorder, korder;
if (omega.x > 0.0) iorder = chi_math::Range<int64_t>(0, Nx);
else iorder = chi_math::Range<int64_t>(Nx - 1, -1, -1);
if (omega.y > 0.0) jorder = chi_math::Range<int64_t>(0, Ny);
else jorder = chi_math::Range<int64_t>(Ny - 1, -1, -1);
if (omega.z > 0.0) korder = chi_math::Range<int64_t>(0, Nz);
else korder = chi_math::Range<int64_t>(Nz - 1, -1, -1);
for (auto i: iorder)
for (auto j: jorder)
for (auto k: korder)
}
};
chi::log.Log() << "Starting iterations" << std::endl;
for (size_t iter=0; iter<200; ++iter)
{
phi_new.assign(phi_new.size(), 0.0);
source_moments = SetSource(grid, sdm, phi_uk_man,
q_source, phi_old, xs, m_ell_em_map);
Sweep();
const double rel_change = ComputeRelativePWChange(grid, sdm, phi_uk_man,
phi_new, phi_old);
std::stringstream outstr;
outstr << "Iteration " << std::setw(5) << iter << " ";
{
char buffer[100];
sprintf(buffer, "%11.3e\n", rel_change);
outstr << buffer;
}
chi::log.Log() << outstr.str();
phi_old = phi_new;
if (rel_change < 1.0e-6 and iter > 0)
break;
}
const size_t num_m0_dofs = sdm.GetNumLocalDOFs(m0_uk_man);
std::vector<double> m0_phi(num_m0_dofs, 0.0);
sdm.CopyVectorWithUnknownScope(phi_old,
m0_phi,
phi_uk_man,
0,
m0_uk_man,
0);
auto phi_ff = std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
);
phi_ff->UpdateFieldVector(m0_phi);
phi_ff->ExportToVTK("SimTest_06_WDD");
chi::Finalize();
return 0;
}
int main(int argc, char **argv)
size_t GetNumGlobalDOFs(const UnknownManager &unknown_manager) const
const UnknownManager UNITARY_UNKNOWN_MANAGER
MeshAttributes Attributes() const
std::array< size_t, 3 > GetIJKInfo() const
std::vector< chi_mesh::Vector3 > MakeCellOrthoSizes() const
chi_data_types::NDArray< uint64_t > MakeIJKToGlobalIDMapping() const
size_t GetGlobalNumberOfCells() const
chi_mesh::MeshContinuumPtr & GetGrid() const
std::shared_ptr< SpatialDiscretization > SDMPtr
MeshHandler & GetCurrentHandler()


![]() equations. For a complete tutorial, on how these equations are derived, please consult this whitepaper.
equations. For a complete tutorial, on how these equations are derived, please consult this whitepaper.![]()
![]()
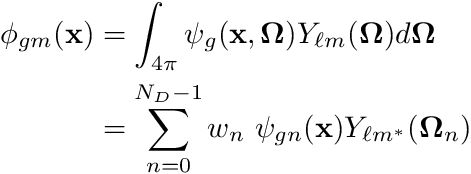
![]() plane, it was generally preferred to use quadratures with even-amounts of quadrature points. Because of this, people in the transport community typically referred to the DO-method as the
plane, it was generally preferred to use quadratures with even-amounts of quadrature points. Because of this, people in the transport community typically referred to the DO-method as the ![]() method with
method with ![]() being the first even quadrature used, followed by
being the first even quadrature used, followed by ![]() etc.
etc.![]() then the azimuthal "level" closest to the equator will start with
then the azimuthal "level" closest to the equator will start with ![]() number of azimuthal angles. For example, an
number of azimuthal angles. For example, an ![]() angular quadrature in 3D has 4 polar levels per octant, therefore the azimuthal angles would start at 4, then 3, then 2, then 1 at the polar-lelel closest to the pole.
angular quadrature in 3D has 4 polar levels per octant, therefore the azimuthal angles would start at 4, then 3, then 2, then 1 at the polar-lelel closest to the pole.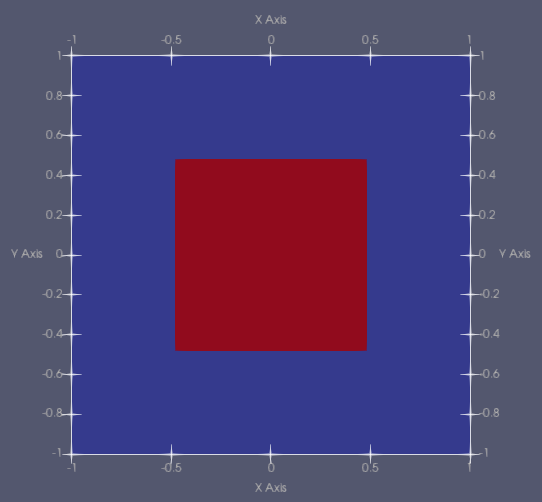
![]()
![]()
![]() is called the Moment-To-Discrete operator (on a nodal level) and defined as
is called the Moment-To-Discrete operator (on a nodal level) and defined as ![]()
![]() is mapped from
is mapped from ![]() . This operator can be precomputed once the angular quadrature is known. The other quantity introduced here,
. This operator can be precomputed once the angular quadrature is known. The other quantity introduced here, ![]() , is called the source moments for cell
, is called the source moments for cell ![]() group
group ![]() and is defined by
and is defined by ![\[ q_{c,g}^{moms,m} = \begin{cases} \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g,c} \ \phi_{mg',c} \biggr] + q_{c,g} \quad \quad &m=0,\\ \sum_{g'=0}^{N_G-1} \biggr[ \sigma_{s\ell,g'{\to}g,c} \ \phi_{mg',c} \biggr] \quad \quad &m\ne 0 \end{cases} \]](../../form_219.png)
![]()
![]()
![]()
![]() .
.
![]() being either
being either ![]() or
or ![]() depending on the sign of
depending on the sign of ![]() . The
. The ![]() of the current cell would then be the downstream flux,
of the current cell would then be the downstream flux, ![]() of the adjacent cell at the interstitial face. With some manipulation we arrive at the following equations to solve the current cell's
of the adjacent cell at the interstitial face. With some manipulation we arrive at the following equations to solve the current cell's ![]() :
:
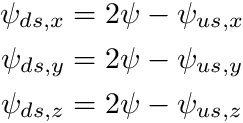
![]() as either the upstream cell's
as either the upstream cell's ![]() or from the upstream boundary condition. Then to solve for the cell
or from the upstream boundary condition. Then to solve for the cell ![]() . Then to compute
. Then to compute ![]() .
.![]() , is maintained. This process is known as sweeping. And for orthogonal grids it looks like shown in the figure below
, is maintained. This process is known as sweeping. And for orthogonal grids it looks like shown in the figure below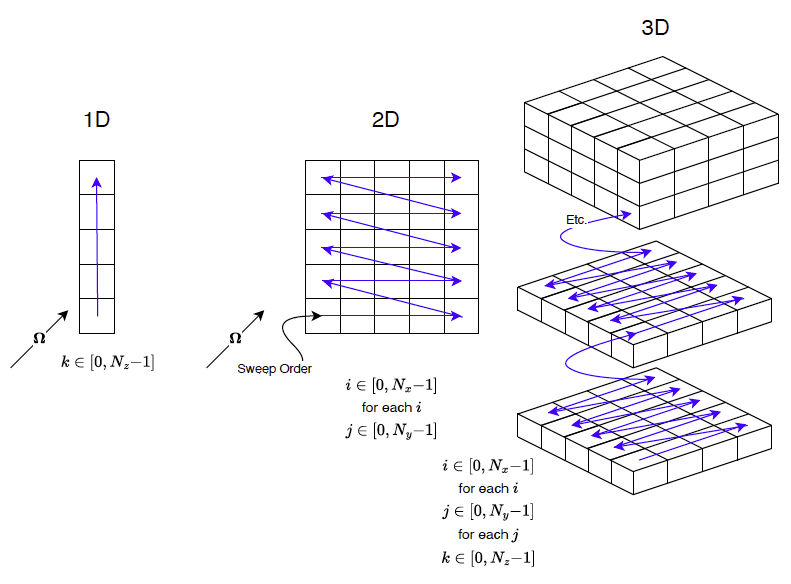
![]() ,
, ![]() and
and ![]() . We finally also assign the dimensionality of the mesh to an integer
. We finally also assign the dimensionality of the mesh to an integer ![]() to
to ![]() in the structure
in the structure ![]() and
and ![]() . Then transport cross sections via the class
. Then transport cross sections via the class ![]() structures. These data structures are multidimensional arrays
structures. These data structures are multidimensional arrays ![]()
![]() ,
, 
![]()
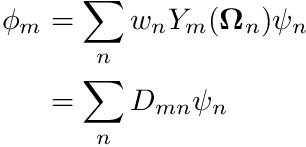
![]() is the Discrete-To-Moment operator. We do the above with the following code
is the Discrete-To-Moment operator. We do the above with the following code ![]() norm by compute the maximum change relative to the scalar moment flux on each node-group pair.
norm by compute the maximum change relative to the scalar moment flux on each node-group pair.