Table of contents
1 Ghost cell's in ChiTech
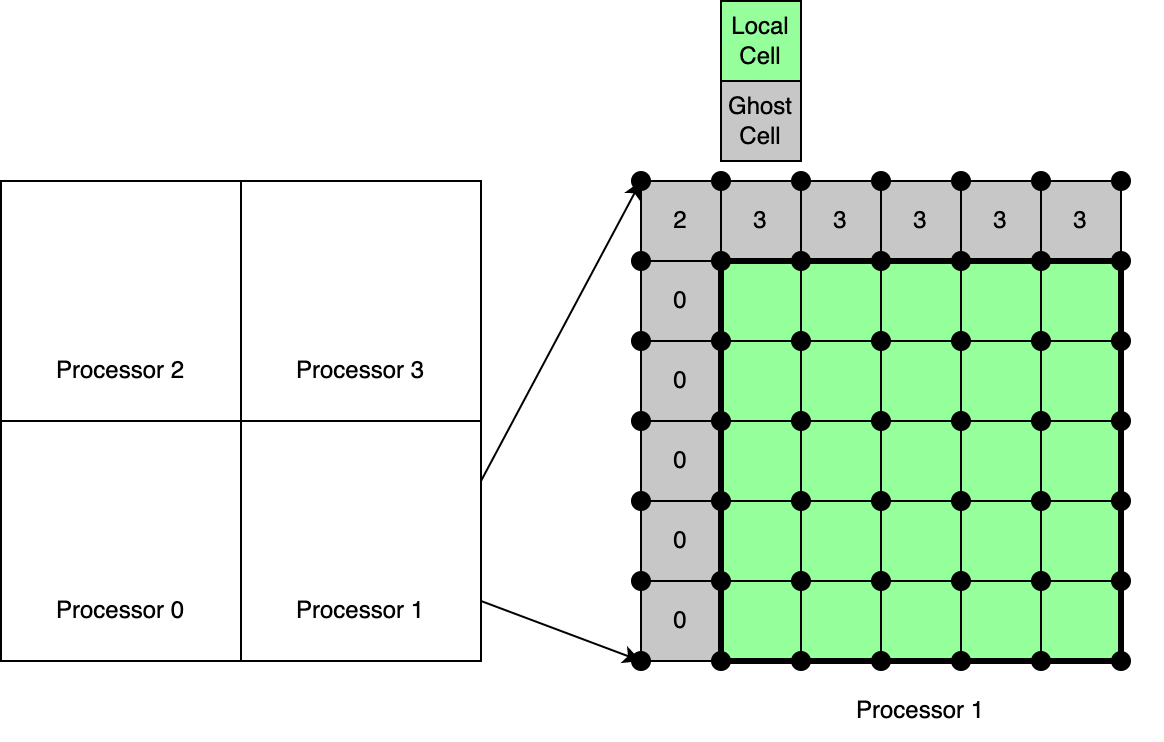
For the discussions that follow refer to the schematic in the figure below.
The concept of ghost cells is quite important in ChiTech, as is the case with any scientific computing library that runs in parallel. Ghost cells arises because it is often required to partition a mesh among different processors in order to more effectively leverage the distributed memory models of HPCs.
Definition: In ChiTech a ghost cell is a cell that shares a face or a vertex with cells partitioned to be local to a given processor. We can observe these cells in the schematic above. This definition requires us to store the first layer of cells beyond the locally owned cells, as well as their accompanying vertices. This allows us to have the complete geometrical information of those ghost cells. Because some numerical schemes often require us to map indices to ghost nodes/cells, this storage scheme, is considered very much necessary.
In this coding tutorial we will be looking at the basics of using the spatial discretization methods (SD methods) to gain access to ghost data, which can be very difficult.
2 Computing the gradient of a Finite Volume Scalar
In the finite volume SD scheme the computation of the gradient of a scalar quantity can often be required. We will use Coding Tutorial 1 - Poisson's problem with Finite Volume as a reference for this tutorial and assume that we are adding code to this tutorial.
Given that we want 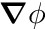 , how do we do this in ChiTech for the Finite Volume SD? Well the first thing to do is to note that, from Gauss's Divergence Theorem,
, how do we do this in ChiTech for the Finite Volume SD? Well the first thing to do is to note that, from Gauss's Divergence Theorem,
![\[ \int_V \boldsymbol{\nabla} \phi dV = \int_S \mathbf{n} \phi dA \]](../../form_148.png)
Now, if the storage of  also follows the Finite Volume SD, then
also follows the Finite Volume SD, then  will be constant on cell
will be constant on cell 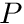 , therefore
, therefore
![\[ \int_S \mathbf{n} \phi dA = V_P \biggr( \boldsymbol{\nabla} \phi \biggr)_P \]](../../form_149.png)
from which we can discretize the surface integral to get
![\[ \biggr( \boldsymbol{\nabla} \phi \biggr)_P = \frac{1}{V_P} \sum_f A_f \mathbf{n}_f \phi_f \]](../../form_150.png)
Now our first problem is to find 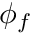 , considering additionally that we might not have an equally spaced mesh. Consider the diagram below
, considering additionally that we might not have an equally spaced mesh. Consider the diagram below
we can now define 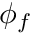 as a geometrically weighted average of
as a geometrically weighted average of 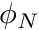 and
and 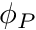 by using the face centroid,
by using the face centroid, 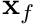 . Therefore,
. Therefore,
![\[ \phi_f = \frac{1}{|| \mathbf{x}_N - \mathbf{x}_P ||} \biggr( (|| \mathbf{x}_N - \mathbf{x}_f ||) \phi_P + (|| \mathbf{x}_f - \mathbf{x}_P ||) \phi_N \biggr) \]](../../form_152.png)
Here we can see that we would have a problem if 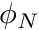 is not locally available, i.e., it is a ghost value. Therefore we need a means to obtain this value.
is not locally available, i.e., it is a ghost value. Therefore we need a means to obtain this value.
3 Making a ghosted vector and communicating ghosted data
Ghost value communication is handled via a chi_math::VectorGhostCommunicator object. These objects require quite a bit of MPI communication during initializing but thereafter can be re-used efficiently on different vectors (as long as they share the intended structure of the ghost-communicator).
In order to gain access to chi_math::VectorGhostCommunicator we first include the header
Next we add the following code:
std::vector<int64_t> ghost_ids = sdm.GetGhostDOFIndices(OneDofPerNode);
num_globl_dofs,
ghost_ids,
std::vector<double> field_wg = vgc.MakeGhostedVector(field);
vgc.CommunicateGhostEntries(field_wg);
static chi::MPI_Info & mpi
The first item on the agenda is "what ghost data to include in a local vector?". To obtain the relevant ghost DOF-ids we ask the SD to provide us with the necessary information with a call to chi_math::SpatialDiscretization::GetGhostDOFIndices. Note this routine requires as a parameter a structure of unknowns, which is why we supply the configuration OneDofPerNode.
Next we construct the chi_math::VectorGhostCommunicator. The constructor of this object requires the number of local DOFs, the number of global DOFs, and the global-ids of the ghosted data. Finally a communicator specification is required. The construction of this object initializes data structures that will make repeated communications very efficient.
Given that we now have the ghost-communicator we can now create a vector that has enough space for the local data AND the ghost data. This is done with a call to chi_math::VectorGhostCommunicator::MakeGhostedVector which is overloaded to accept a vector containing only local data. This allows us, in this case, to make a ghosted vector, field_wg, with the local entries the same as field but with additional zeros representing the ghost values.
Finally we communicate ghost entries, of a given vector, with a call to chi_math::VectorGhostCommunicator::CommunicateGhostEntries. Next we will look at how we are going to access the ghost values.
4 Accessing ghosted data
As a reminder, consider that a call to chi_math::SpatialDiscretization::MapDOF provides the global-id of a DOF whereas chi_math::SpatialDiscretization::MapDOFLocal provides the local-id of a DOF. Ghost data is, by its nature, not normally a local quantity. Therefore, one would assume that a call to MapDOFLocal would provide an invalid address for ghost-DOFs, however, there is a catch. The id provided by MapDOFLocal maps to a location aligned with the call to GetGhostDOFIndices. For example, consider there are 100 local-DOFs, and 15 ghost-DOFs on a given processor. A call to GetGhostDOFIndices would return 15 indices. Now lets say we want the local-id of the 9-th ghost-DOF. In this case a call to MapDOFLocal will return 100+8, because the 9-th ghost-DOF has an index of 8 in the list of ghost-ids.
We will now use this concept in the computation of the gradient of 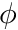 .
.
First we create a vector that can store the x, y and z components of the gradient. The size of this vector, as well as mappings into it, will be provided by the SD and therefore we need to make a chi_math::UnknownManager to dictate the structure of the unknowns. Therefore we do the following:
Next we get the size of the vector and instantiate it
const size_t num_grad_dofs = sdm.GetNumLocalDOFs(grad_uk_man);
std::vector<double> grad_phi(num_grad_dofs, 0.0);
Since we already have ghosted data we are now ready to compute the gradient on a cell-by-cell basis. We do this with the following code:
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const int64_t imap = sdm.MapDOFLocal(cell, 0);
const double phi_P = field_wg[imap];
const auto& xp = cell.centroid;
size_t f=0;
for (const auto& face : cell.faces)
{
const auto& xf = face.centroid;
const auto Af = cell_mapping.FaceArea(f) * face.normal;
double phi_N = 0.0;
auto xn = xp + 2*(xf-xp);
if (face.has_neighbor)
{
const auto& adj_cell = grid.cells[face.neighbor_id];
const int64_t nmap = sdm.MapDOFLocal(adj_cell, 0);
phi_N = field_wg[nmap];
xn = adj_cell.centroid;
}
grad_phi_P += Af * ((xn-xf).Norm()*phi_P + (xf-xp).Norm()*phi_N)/
(xn-xp).Norm();
++f;
}
grad_phi_P /= cell_mapping.CellVolume();
const int64_t xmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 0);
const int64_t ymap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 1);
const int64_t zmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 2);
grad_phi[xmap] = grad_phi_P.x;
grad_phi[ymap] = grad_phi_P.y;
grad_phi[zmap] = grad_phi_P.z;
}
As per usual we loop over the local cells. Once we have a cell reference we obtain a cell-mapping. We then immediately grab the present cell's 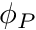 value by first mapping its address (reminder, the second paramater of
value by first mapping its address (reminder, the second paramater of MapDOFLocal is the node-number, which is zero for the Finite Volume SD), then accessing the ghosted field vector, field_wg.
We then initialize an, initially zero, three-component vector representing the gradient for cell 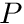 . Next we proceed to loop over the faces of the cell where we obtain the neighboring cell's
. Next we proceed to loop over the faces of the cell where we obtain the neighboring cell's 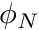 value (provided that
value (provided that face.has_neighbor, otherwise defaulting to the boundary condition of zero) with the code
const auto& adj_cell = grid.cells[face.neighbor_id];
const int64_t nmap = sdm.MapDOFLocal(adj_cell, 0);
phi_N = field_wg[nmap];
Notice here the use of MapDOFLocal. This only works because field_wg will have a value for the case when MapDOFLocal is asked to map a ghosted DOF.
Finally we compute the gradient from the formula
![\[ \phi_f = \frac{1}{|| \mathbf{x}_N - \mathbf{x}_P ||} \biggr( (|| \mathbf{x}_N - \mathbf{x}_f ||) \phi_P + (|| \mathbf{x}_f - \mathbf{x}_P ||) \phi_N \biggr) \]](../../form_152.png)
with the code
grad_phi_P += Af * ((xn-xf).Norm()*phi_P + (xf-xp).Norm()*phi_N)/
(xn-xp).Norm();
which is divided by the volume at the termination of the faces-loop.
The final step for a cell is to appropriately store this gradient, therefore we map each component of the gradient and appropriately set the grad_phi vector,
const int64_t xmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 0);
const int64_t ymap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 1);
const int64_t zmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 2);
grad_phi[xmap] = grad_phi_P.x;
grad_phi[ymap] = grad_phi_P.y;
grad_phi[zmap] = grad_phi_P.z;
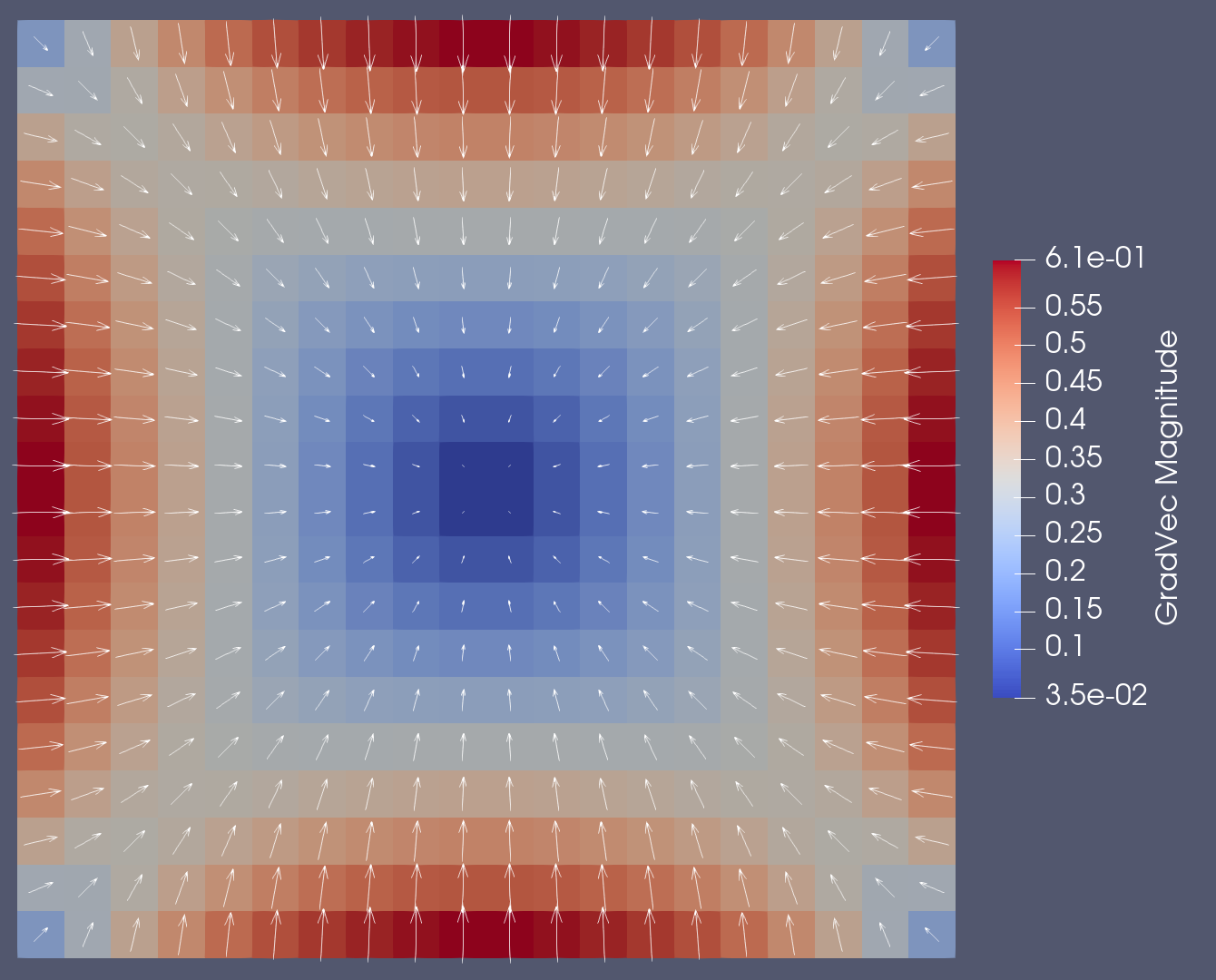
5 Visualizing the gradient
Visualizing the gradient is conceptually simple. We simply create a field-function that will export all three the components of the gradient together. Then we use paraview to make arrow glyphs for visualization.
auto ff_grad = std::make_shared<chi_physics::FieldFunction>(
"GradPhi",
sdm_ptr,
);
ff_grad->UpdateFieldVector(grad_phi);
ff_grad->ExportToVTK("CodeTut2_FV_grad");
Within paraview we can use the Calculator filter to construct vector quantities from the 3 components after which we can apply a Glyph filter to obtain a visualization as shown below
The complete program
#include "math/SpatialDiscretization/FiniteVolume/fv.h"
#include "physics/FieldFunction/fieldfunction2.h"
int main(
int argc,
char* argv[])
{
chi::Initialize(argc,argv);
chi::RunBatch(argc, argv);
chi::log.Log() << "Coding Tutorial 2";
const auto& grid = *grid_ptr;
chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
typedef std::shared_ptr<chi_math::SpatialDiscretization>
SDMPtr;
SDMPtr sdm_ptr = chi_math::SpatialDiscretization_FV::New(grid_ptr);
const auto& sdm = *sdm_ptr;
const auto& OneDofPerNode = sdm.UNITARY_UNKNOWN_MANAGER;
const size_t num_local_dofs = sdm.GetNumLocalDOFs(OneDofPerNode);
const size_t num_globl_dofs = sdm.GetNumGlobalDOFs(OneDofPerNode);
chi::log.Log() << "Num local DOFs: " << num_local_dofs;
chi::log.Log() << "Num globl DOFs: " << num_globl_dofs;
const auto n = static_cast<int64_t>(num_local_dofs);
const auto N = static_cast<int64_t>(num_globl_dofs);
std::vector<int64_t> nodal_nnz_in_diag;
std::vector<int64_t> nodal_nnz_off_diag;
sdm.BuildSparsityPattern(nodal_nnz_in_diag,nodal_nnz_off_diag,OneDofPerNode);
nodal_nnz_in_diag,
nodal_nnz_off_diag);
chi::log.Log() << "Assembling system: ";
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const int64_t imap = sdm.MapDOF(cell,0);
const auto& xp = cell.centroid;
const double V = cell_mapping.CellVolume();
size_t f=0;
for (const auto& face : cell.faces)
{
const auto Af = face.normal * cell_mapping.FaceArea(f);
if (face.has_neighbor)
{
const auto& adj_cell = grid.cells[face.neighbor_id];
const int64_t jnmap = sdm.MapDOF(adj_cell,0);
const auto& xn = adj_cell.centroid;
const auto xpn = xn - xp;
const auto cf = Af.Dot(xpn) / xpn.NormSquare();
MatSetValue(A, imap, imap , cf, ADD_VALUES);
MatSetValue(A, imap, jnmap, -cf, ADD_VALUES);
}
else
{
const auto& xn = xp + 2.0*(face.centroid - xp);
const auto xpn = xn - xp;
const auto cf = Af.Dot(xpn) / xpn.NormSquare();
MatSetValue(A, imap, imap , cf, ADD_VALUES);
}
++f;
}
VecSetValue(b, imap, 1.0*V, ADD_VALUES);
}
chi::log.Log() << "Global assembly";
MatAssemblyBegin(A, MAT_FINAL_ASSEMBLY);
MatAssemblyEnd(A, MAT_FINAL_ASSEMBLY);
VecAssemblyBegin(b);
VecAssemblyEnd(b);
chi::log.Log() << "Done global assembly";
chi::log.Log() << "Solving: ";
auto petsc_solver =
A,
"FVDiffSolver",
KSPCG,
PCGAMG,
1.0e-6,
1000);
KSPSolve(petsc_solver.ksp,b,x);
chi::log.Log() << "Done solving";
std::vector<double> field(num_local_dofs, 0.0);
sdm.LocalizePETScVector(x,field,OneDofPerNode);
KSPDestroy(&petsc_solver.ksp);
VecDestroy(&x);
VecDestroy(&b);
MatDestroy(&A);
chi::log.Log() << "Done cleanup";
auto ff = std::make_shared<chi_physics::FieldFunction>(
"Phi",
sdm_ptr,
);
ff->UpdateFieldVector(field);
ff->ExportToVTK("CodeTut2_FV");
std::vector<int64_t> ghost_ids = sdm.GetGhostDOFIndices(OneDofPerNode);
num_globl_dofs,
ghost_ids,
std::vector<double> field_wg = vgc.MakeGhostedVector(field);
vgc.CommunicateGhostEntries(field_wg);
const size_t num_grad_dofs = sdm.GetNumLocalDOFs(grad_uk_man);
std::vector<double> grad_phi(num_grad_dofs, 0.0);
for (const auto& cell : grid.local_cells)
{
const auto& cell_mapping = sdm.GetCellMapping(cell);
const int64_t imap = sdm.MapDOFLocal(cell, 0);
const double phi_P = field_wg[imap];
const auto& xp = cell.centroid;
size_t f=0;
for (const auto& face : cell.faces)
{
const auto& xf = face.centroid;
const auto Af = cell_mapping.FaceArea(f) * face.normal;
double phi_N = 0.0;
auto xn = xp + 2*(xf-xp);
if (face.has_neighbor)
{
const auto& adj_cell = grid.cells[face.neighbor_id];
const int64_t nmap = sdm.MapDOFLocal(adj_cell, 0);
phi_N = field_wg[nmap];
xn = adj_cell.centroid;
}
grad_phi_P += Af * ((xn-xf).Norm()*phi_P + (xf-xp).Norm()*phi_N)/
(xn-xp).Norm();
++f;
}
grad_phi_P /= cell_mapping.CellVolume();
const int64_t xmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 0);
const int64_t ymap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 1);
const int64_t zmap = sdm.MapDOFLocal(cell, 0, grad_uk_man, 0, 2);
grad_phi[xmap] = grad_phi_P.x;
grad_phi[ymap] = grad_phi_P.y;
grad_phi[zmap] = grad_phi_P.z;
}
auto ff_grad = std::make_shared<chi_physics::FieldFunction>(
"GradPhi",
sdm_ptr,
);
ff_grad->UpdateFieldVector(grad_phi);
ff_grad->ExportToVTK("CodeTut2_FV_grad");
chi::Finalize();
return 0;
}
int main(int argc, char **argv)
chi_mesh::MeshContinuumPtr & GetGrid() const
void InitMatrixSparsity(Mat &A, const std::vector< int64_t > &nodal_nnz_in_diag, const std::vector< int64_t > &nodal_nnz_off_diag)
PETScSolverSetup CreateCommonKrylovSolverSetup(Mat ref_matrix, const std::string &in_solver_name="KSPSolver", const std::string &in_solver_type=KSPGMRES, const std::string &in_preconditioner_type=PCNONE, double in_relative_residual_tolerance=1.0e-6, int64_t in_maximum_iterations=100)
Mat CreateSquareMatrix(int64_t local_size, int64_t global_size)
Vec CreateVector(int64_t local_size, int64_t global_size)
std::shared_ptr< SpatialDiscretization > SDMPtr
MeshHandler & GetCurrentHandler()


![]() , how do we do this in ChiTech for the Finite Volume SD? Well the first thing to do is to note that, from Gauss's Divergence Theorem,
, how do we do this in ChiTech for the Finite Volume SD? Well the first thing to do is to note that, from Gauss's Divergence Theorem, ![]()
![]() also follows the Finite Volume SD, then
also follows the Finite Volume SD, then ![]() will be constant on cell
will be constant on cell ![]() , therefore
, therefore ![]()
![]()
![]() , considering additionally that we might not have an equally spaced mesh. Consider the diagram below
, considering additionally that we might not have an equally spaced mesh. Consider the diagram below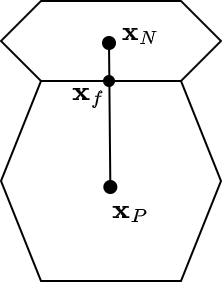
![]() as a geometrically weighted average of
as a geometrically weighted average of ![]() and
and ![]() by using the face centroid,
by using the face centroid, ![]() . Therefore,
. Therefore, ![]()
![]() is not locally available, i.e., it is a ghost value. Therefore we need a means to obtain this value.
is not locally available, i.e., it is a ghost value. Therefore we need a means to obtain this value.![]() .
.![]() value by first mapping its address (reminder, the second paramater of
value by first mapping its address (reminder, the second paramater of ![]() . Next we proceed to loop over the faces of the cell where we obtain the neighboring cell's
. Next we proceed to loop over the faces of the cell where we obtain the neighboring cell's ![]() value (provided that
value (provided that ![]()