Coding Tutorial 4 - MMS for Poisson's problem with PWLC

Table of contents

• 1 Defining a wrapper to call a lua function
• 2 Lua functions
• 3 Getting guadrature-point real world XYZ
• 4 Convergence study
• The complete program

1 Defining a wrapper to call a lua function

To implement a manufactured solution in our PWLC solver from Coding Tutorial 3 - Poisson's problem with PWLC we are required to call a lua-function with spatial coordinates x,y,z. In order to use the lua-console, specifically the lua state, we have to include the headers

#include "console/chi_console.h"
#include "chi_lua.h"

When then have to grab the console state from the runtime environment. To do this we add the following code, in the beginning of the program, just below chi::RunBatch

auto L = chi::console.consoleState;

Next we have to tell the c++ code exactly how to call a lua-function. To this end we define a wrapper using a c++ lambda as shown below. You can define this function where ever you like as long as it can capture the lua state, L. For this tutorial we defined it just before the matrix assembly.

auto CallLuaXYZFunction = [&L](const std::string& lua_func_name,
                               const chi_mesh::Vector3& xyz)
{
  //============= Load lua function
  lua_getglobal(L, lua_func_name.c_str());
 
  //============= Error check lua function
  if (not lua_isfunction(L, -1))
    throw std::logic_error("CallLuaXYZFunction attempted to access lua-function, " +
                           lua_func_name + ", but it seems the function"
                                           " could not be retrieved.");
 
  //============= Push arguments
  lua_pushnumber(L, xyz.x);
  lua_pushnumber(L, xyz.y);
  lua_pushnumber(L, xyz.z);
 
  //============= Call lua function
  //3 arguments, 1 result (double), 0=original error object
  double lua_return = 0.0;
  if (lua_pcall(L,3,1,0) == 0)
  {
    LuaCheckNumberValue("CallLuaXYZFunction", L, -1);
    lua_return = lua_tonumber(L,-1);
  }
  else
    throw std::logic_error("CallLuaXYZFunction attempted to call lua-function, " +
                           lua_func_name + ", but the call failed." +
                           xyz.PrintStr());
 
  lua_pop(L,1); //pop the double, or error code
 
  return lua_return;
};

Notice this function takes 2 arguments: a string value representing the lua function's name, and a chi_mesh::Vector3 indicating the real-word XYZ coordinates at which to evaluate the function.

In order to implement a manufactures solution we need a right-hand-side (RHS) function and an actual manufactured solution (MS) function. The RHS function will essentially steer the entire solution towards the manufactured solution. The evaluation of the actual manufactured solution is required in two places, i.e., in the implementation of Dirichlet boundary conditions, and when we compute the L2-norm of the error between our FEM-solution and the manufactured one.

2 Lua functions

The RHS function and the MS function both need to exist within the lua state. We therefore ad the following to the mesh.lua input file.

function MMS_phi(x,y,z)
    return math.cos(math.pi*x) + math.cos(math.pi*y)
end
function MMS_q(x,y,z)
    return math.pi*math.pi * (math.cos(math.pi*x)+math.cos(math.pi*y))
end

The function MMS_phi is the MS function and the function MMS_q is the RHS function. These functions can be defined anywhere in the input file as long as they are available in the state when solver needs them.

3 Getting guadrature-point real world XYZ

Quadrautre-point real-world positions are stored when the qp_data structure is created. They are accessed with the call chi_math::finite_element::InternalQuadraturePointData::QPointXYZ, taking the quadrature point index as a parameter.

for (size_t qp : qp_data.QuadraturePointIndices())
  cell_rhs[i] += CallLuaXYZFunction(qp_data.QPointXYZ(qp),"MMS_q", L) *
                 qp_data.ShapeValue(i, qp) * qp_data.JxW(qp);

4 Convergence study

The Method of Manufactured Solution (MMS) is often used to verify the rate of convergence of computational methods. In order to determine magnitude of the error of the FEM solution, 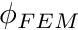, compared to the MS, 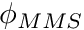, we need to evaluate the following norm

We again here use the quadrature rules to obtain this integral as

for which we use the code

//============================================= Compute error
//First get ghosted values
const auto field_wg = ff->GetGhostedFieldVector();
 
double local_error = 0.0;
for (const auto& cell : grid.local_cells)
{
  const auto& cell_mapping = sdm.GetCellMapping(cell);
  const size_t num_nodes = cell_mapping.NumNodes();
  const auto qp_data = cell_mapping.MakeVolumeQuadraturePointData();
 
  //======================= Grab nodal phi values
  std::vector<double> nodal_phi(num_nodes,0.0);
  for (size_t j=0; j < num_nodes; ++j)
  {
    const int64_t imap = sdm.MapDOFLocal(cell, j);
    nodal_phi[j] = field_wg[imap];
  }//for j
 
  //======================= Quadrature loop
  for (size_t qp : qp_data.QuadraturePointIndices())
  {
    double phi_fem = 0.0;
    for (size_t j=0; j < num_nodes; ++j)
      phi_fem += nodal_phi[j] * qp_data.ShapeValue(j, qp);
 
    double phi_true = CallLuaXYZFunction("MMS_phi",qp_data.QPointXYZ(qp));
 
    local_error += std::pow(phi_true - phi_fem,2.0) * qp_data.JxW(qp);
  }
}//for cell
 
double global_error = 0.0;
MPI_Allreduce(&local_error,     //sendbuf
              &global_error,    //recvbuf
              1, MPI_DOUBLE,    //count+datatype
              MPI_SUM,          //operation
              Chi::mpi.comm);  //communicator
 
global_error = std::sqrt(global_error);
 
chi::log.Log() << "Error: " << std::scientific << global_error
               << " Num-cells: " << grid.GetGlobalNumberOfCells();

Notice that we grab the nodal values of 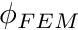before we loop over quadrature points. We then use these nodal values within the quadrature-point loop to construct 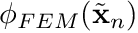as

with the code

for (size_t j=0; j < num_nodes; ++j)
  phi_fem += nodal_phi[j] * qp_data.ShapeValue(j, qp);

Notice also that we first have to compute a local error, from the cells that are on the local partition. This is then followed by an MPI_Allreduce, with the MPI_SUM operation, to gather all the local error values into a single global error value. This is done via the code

double global_error = 0.0;
MPI_Allreduce(&local_error,     //sendbuf
              &global_error,    //recvbuf
              1, MPI_DOUBLE,    //count+datatype
              MPI_SUM,          //operation
              Chi::mpi.comm);  //communicator
 
global_error = std::sqrt(global_error);

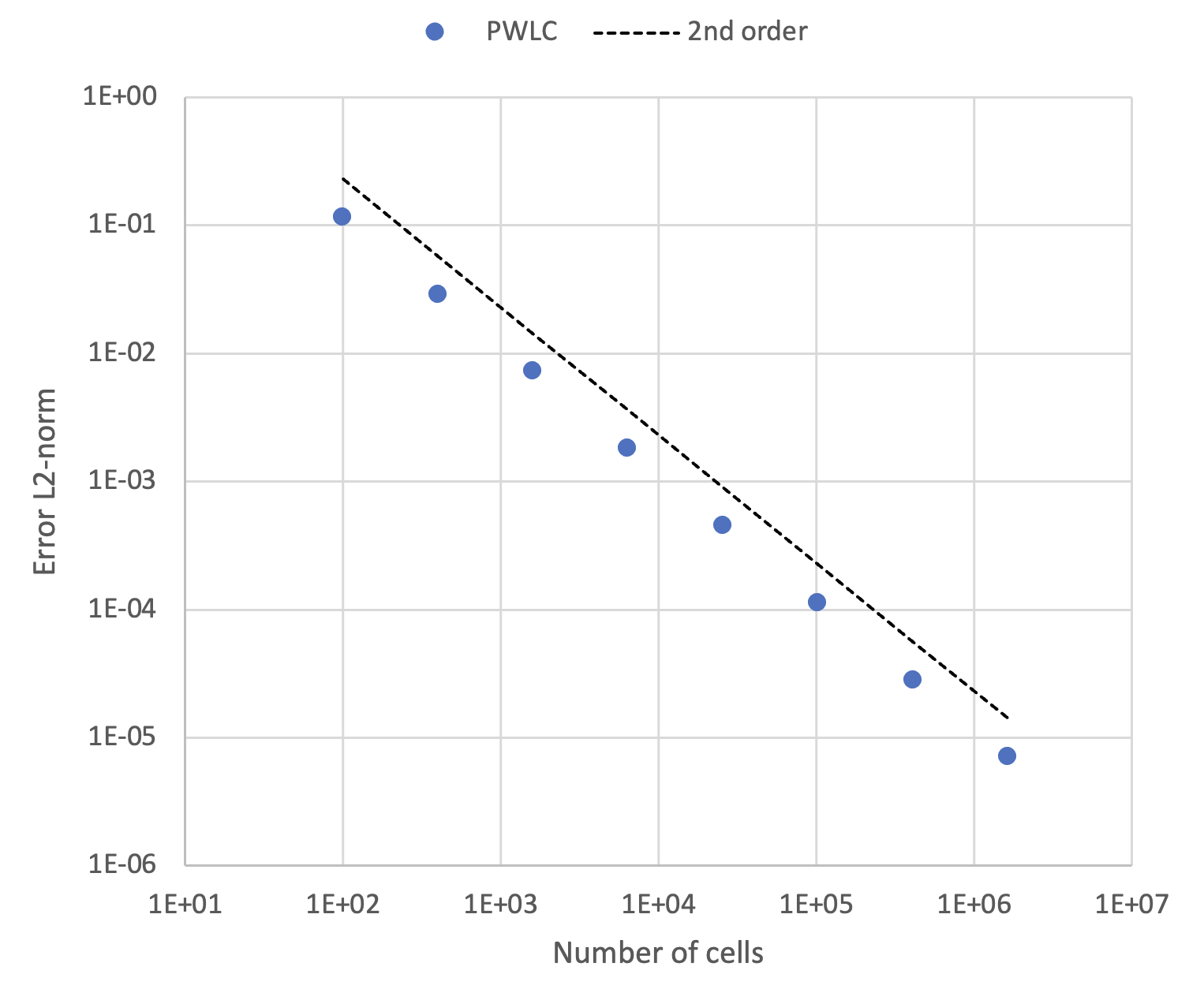
With this code in-place we can run the program several times with a different amount of cells, which provides us with the data below:

The complete program

#include "chi_runtime.h"
#include "chi_log.h"
 
#include "mesh/MeshHandler/chi_meshhandler.h"
 
#include "math/SpatialDiscretization/FiniteElement/PiecewiseLinear/pwlc.h"
#include "math/PETScUtils/petsc_utils.h"
 
#include "physics/FieldFunction/fieldfunction2.h"
 
#include "console/chi_console.h"
#include "chi_lua.h"
 
int main(int argc, char* argv[])
{
  chi::Initialize(argc,argv);
  chi::RunBatch(argc, argv);
 
  chi::log.Log() << "Coding Tutorial 4";
 
  //============================================= Get grid
  auto grid_ptr = chi_mesh::GetCurrentHandler().GetGrid();
  const auto& grid = *grid_ptr;
 
  chi::log.Log() << "Global num cells: " << grid.GetGlobalNumberOfCells();
 
  //============================================= Make SDM
  typedef std::shared_ptr<chi_math::SpatialDiscretization> SDMPtr;
  SDMPtr sdm_ptr = chi_math::SpatialDiscretization_PWLC::New(grid_ptr);
  const auto& sdm = *sdm_ptr;
 
  const auto& OneDofPerNode = sdm.UNITARY_UNKNOWN_MANAGER;
 
  const size_t num_local_dofs = sdm.GetNumLocalDOFs(OneDofPerNode);
  const size_t num_globl_dofs = sdm.GetNumGlobalDOFs(OneDofPerNode);
 
  chi::log.Log() << "Num local DOFs: " << num_local_dofs;
  chi::log.Log() << "Num globl DOFs: " << num_globl_dofs;
 
  //============================================= Initializes Mats and Vecs
  const auto n = static_cast<int64_t>(num_local_dofs);
  const auto N = static_cast<int64_t>(num_globl_dofs);
  Mat A;
  Vec x,b;
 
  A = chi_math::PETScUtils::CreateSquareMatrix(n,N);
  x = chi_math::PETScUtils::CreateVector(n,N);
  b = chi_math::PETScUtils::CreateVector(n,N);
 
  std::vector<int64_t> nodal_nnz_in_diag;
  std::vector<int64_t> nodal_nnz_off_diag;
  sdm.BuildSparsityPattern(nodal_nnz_in_diag,nodal_nnz_off_diag, OneDofPerNode);
 
  chi_math::PETScUtils::InitMatrixSparsity(A,
                                           nodal_nnz_in_diag,
                                           nodal_nnz_off_diag);
 
  //============================================= Source lambda
  auto CallLuaXYZFunction = [&L](const std::string& lua_func_name,
                                 const chi_mesh::Vector3& xyz)
  {
    //============= Load lua function
    lua_getglobal(L, lua_func_name.c_str());
 
    //============= Error check lua function
    if (not lua_isfunction(L, -1))
      throw std::logic_error("CallLuaXYZFunction attempted to access lua-function, " +
                             lua_func_name + ", but it seems the function"
                                             " could not be retrieved.");
 
    //============= Push arguments
    lua_pushnumber(L, xyz.x);
    lua_pushnumber(L, xyz.y);
    lua_pushnumber(L, xyz.z);
 
    //============= Call lua function
    //3 arguments, 1 result (double), 0=original error object
    double lua_return = 0.0;
    if (lua_pcall(L,3,1,0) == 0)
    {
      LuaCheckNumberValue("CallLuaXYZFunction", L, -1);
      lua_return = lua_tonumber(L,-1);
    }
    else
      throw std::logic_error("CallLuaXYZFunction attempted to call lua-function, " +
                             lua_func_name + ", but the call failed." +
                             xyz.PrintStr());
 
    lua_pop(L,1); //pop the double, or error code
 
    return lua_return;
  };
 
  //============================================= Assemble the system
  chi::log.Log() << "Assembling system: ";
  for (const auto& cell : grid.local_cells)
  {
    const auto& cell_mapping = sdm.GetCellMapping(cell);
    const auto  qp_data      = cell_mapping.MakeVolumeQuadraturePointData();
    const auto  cell_node_xyzs = cell_mapping.GetNodeLocations();
 
    const size_t num_nodes = cell_mapping.NumNodes();
    MatDbl Acell(num_nodes, VecDbl(num_nodes, 0.0));
    VecDbl cell_rhs(num_nodes, 0.0);
 
    for (size_t i=0; i<num_nodes; ++i)
    {
      for (size_t j=0; j<num_nodes; ++j)
      {
        double entry_aij = 0.0;
        for (size_t qp : qp_data.QuadraturePointIndices())
        {
          entry_aij +=
            qp_data.ShapeGrad(i, qp).Dot(qp_data.ShapeGrad(j, qp)) *
            qp_data.JxW(qp);
        }//for qp
        Acell[i][j] = entry_aij;
      }//for j
      for (size_t qp : qp_data.QuadraturePointIndices())
        cell_rhs[i] += CallLuaXYZFunction("MMS_q",qp_data.QPointXYZ(qp)) *
                       qp_data.ShapeValue(i, qp) * qp_data.JxW(qp);
    }//for i
 
    //======================= Flag nodes for being on dirichlet boundary
    std::vector<bool> node_boundary_flag(num_nodes, false);
    const size_t num_faces = cell.faces.size();
    for (size_t f=0; f<num_faces; ++f)
    {
      const auto& face = cell.faces[f];
      if (face.has_neighbor) continue;
 
      const size_t num_face_nodes = face.vertex_ids.size();
      for (size_t fi=0; fi<num_face_nodes; ++fi)
      {
        const uint i = cell_mapping.MapFaceNode(f,fi);
        node_boundary_flag[i] = true;
      }//for fi
    }//for face f
 
    //======================= Develop node mapping
    std::vector<int64_t> imap(num_nodes, 0); //node-mapping
    for (size_t i=0; i<num_nodes; ++i)
      imap[i] = sdm.MapDOF(cell, i);
 
    //======================= Assembly into system
    for (size_t i=0; i<num_nodes; ++i)
    {
      if (node_boundary_flag[i]) //if dirichlet node
      {
        MatSetValue(A, imap[i], imap[i], 1.0, ADD_VALUES);
        double bval = CallLuaXYZFunction("MMS_phi",cell_node_xyzs[i]);
        VecSetValue(b, imap[i], bval, ADD_VALUES);
      }
      else
      {
        for (size_t j=0; j<num_nodes; ++j)
        {
          if (not node_boundary_flag[j])
            MatSetValue(A, imap[i], imap[j], Acell[i][j], ADD_VALUES);
          else
          {
            double bval = CallLuaXYZFunction("MMS_phi",cell_node_xyzs[j]);
            VecSetValue(b, imap[i], -Acell[i][j]*bval, ADD_VALUES);
          }
        }//for j
        VecSetValue(b, imap[i], cell_rhs[i], ADD_VALUES);
      }
    }//for i
  }//for cell
 
  chi::log.Log() << "Global assembly";
 
  MatAssemblyBegin(A, MAT_FINAL_ASSEMBLY);
  MatAssemblyEnd(A, MAT_FINAL_ASSEMBLY);
  VecAssemblyBegin(b);
  VecAssemblyEnd(b);
 
  chi::log.Log() << "Done global assembly";
 
  //============================================= Create Krylov Solver
  chi::log.Log() << "Solving: ";
  auto petsc_solver =
    chi_math::PETScUtils::CreateCommonKrylovSolverSetup(
      A,               //Matrix
      "PWLCDiffSolver",  //Solver name
      KSPCG,           //Solver type
      PCGAMG,          //Preconditioner type
      1.0e-6,          //Relative residual tolerance
      1000);            //Max iterations
 
  //============================================= Solve
  KSPSolve(petsc_solver.ksp,b,x);
 
  chi::log.Log() << "Done solving";
 
  //============================================= Extract PETSc vector
  std::vector<double> field;
  sdm.LocalizePETScVector(x,field,OneDofPerNode);
 
  //============================================= Clean up
  KSPDestroy(&petsc_solver.ksp);
 
  VecDestroy(&x);
  VecDestroy(&b);
  MatDestroy(&A);
 
  chi::log.Log() << "Done cleanup";
 
  //============================================= Create Field Function
  auto ff = std::make_shared<chi_physics::FieldFunction>(
    "Phi",                                           //Text name
    sdm_ptr,                                         //Spatial Discr.
    chi_math::Unknown(chi_math::UnknownType::SCALAR) //Unknown
  );
 
  ff->UpdateFieldVector(field);
 
  ff->ExportToVTK("CodeTut4_PWLC");
 
  //============================================= Compute error
  //First get ghosted values
  const auto field_wg = ff->GetGhostedFieldVector();
 
  double local_error = 0.0;
  for (const auto& cell : grid.local_cells)
  {
    const auto& cell_mapping = sdm.GetCellMapping(cell);
    const size_t num_nodes = cell_mapping.NumNodes();
    const auto qp_data = cell_mapping.MakeVolumeQuadraturePointData();
 
    //======================= Grab nodal phi values
    std::vector<double> nodal_phi(num_nodes,0.0);
    for (size_t j=0; j < num_nodes; ++j)
    {
      const int64_t jmap = sdm.MapDOFLocal(cell, j);
      nodal_phi[j] = field_wg[jmap];
    }//for j
 
    //======================= Quadrature loop
    for (size_t qp : qp_data.QuadraturePointIndices())
    {
      double phi_fem = 0.0;
      for (size_t j=0; j < num_nodes; ++j)
        phi_fem += nodal_phi[j] * qp_data.ShapeValue(j, qp);
 
      double phi_true = CallLuaXYZFunction("MMS_phi",qp_data.QPointXYZ(qp));
 
      local_error += std::pow(phi_true - phi_fem,2.0) * qp_data.JxW(qp);
    }
  }//for cell
 
  double global_error = 0.0;
  MPI_Allreduce(&local_error,     //sendbuf
                &global_error,    //recvbuf
                1, MPI_DOUBLE,    //count+datatype
                MPI_SUM,          //operation
                Chi::mpi.comm);  //communicator
 
  global_error = std::sqrt(global_error);
 
  chi::log.Log() << "Error: " << std::scientific << global_error
                 << " Num-cells: " << grid.GetGlobalNumberOfCells();
 
  chi::Finalize();
  return 0;
}